I had no intention to discuss the Ramanujan Machine again, but over the past few days there has been a flurry of (attempted) trollish comments on that post, so after taking a brief look at the latest version, I thought I would offer you my updates. (I promise for the last time.)
Probably the nicest thing I have to say about the updated paper is that it is better than the original. My complaints about the tone of the paper remain the same, but I don’t think it is necessary for me to revisit them here.
Concerning the intellectual merit, I think it is worth making the following remarks. First, I am only address the contributions to mathematics, Second, what counts as a new conjecture is not really as obvious as it sounds. Since continued fractions are somewhat recherché, it might be more helpful to give an analogy with infinite series. Suppose I claimed it was a new result that
\( \displaystyle{ 2G = \sum_{n=0}^{\infty} a_n = 1 + \frac{1}{2} + \frac{5}{36} + \frac{5}{72} + \frac{269}{3600} – \frac{1219}{705600} + \ldots } \)
where for \(n \ge 4\) one has
\(2 n^2 a_n = n^2 a_{n-1} – 2 (n-2)^2 a_{n-2} + (n-2)^2 a_{n-3}.\)
How can you evaluate this claim? Quite probably this is the first time this result has been written down, and you will not find it anywhere in the literature. But it turns out that
\( \displaystyle{ \left(\sum_{n=0}^{\infty} \frac{x^n}{2^n} \right) \times \left(\sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)^2} \right)
= \sum_{n=0}^{\infty} a_n x^n}\)
and letting \(x=1\) recovers the identity above and immediately explains how to prove it. To a mathematician, it is clear that the proof explains not only why the originally identity is true, but also why it is not at all interesting. It arises as more or less a formal manipulation of a definition, with a few minor things thrown in like the sum of a geometric series and facts about which functions satisfy certain types of ordinary differential equations. The point is that the identities produced by the Ramanujan Machine have all been of this type. That is, upon further scrutiny, they have not yet revealed any new mathematical insights, even if any particular example, depending on what you know, may be more or less tricky to compute.
What then about the improved irrationality measures for the Catalan constant? I think that is a polite way of describing a failed attempt to prove that Catalan’s constant was irrational. It’s something that would be only marginally publishable in a mathematics journal even with a proof. Results about the irrationality measure in the range where they are irrational have genuine implications about the arithmetic of the relevant numbers, but these results do not.
What then about the new continued fractions developed over the last year — maybe these are now deeper? Here you have to remember that continued fractions, especially of the kind considered in this paper, are more or less equivalent to questions about certain types of ordinary differential equations and their related periods. (But importantly, not conversely: most of these interesting ODEs have nothing to do with continued fractions since they are associated with recurrences of length greater than two.) For your sake, dear reader, I voluntarily chose to give up an hour or two of my life and took a closer look at one of their “new conjectures.” I deliberately chose one that they specifically highlighted in their paper, namely:
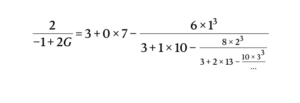
Where \(G\) here is Catalan’s constant \(L(2,\chi_4)\). As you might find unsurprising, once you start to unravel what is going on you find that, just as in the example above, the mystery of these numbers goes away. This example can be generalized in a number of ways without much change to the argument. Let \(p_0=1\) and \(q_0 = 0\), and otherwise let
\(\displaystyle{\frac{p_n}{q_n} = \frac{3}{1}, \frac{33}{13}, \frac{765}{313}, \frac{30105}{12453}, \frac{1790775}{743403}, \ldots} \)
denote the (non-reduced) partial fraction convergents. If
\( \displaystyle{ P(z) = \sum \frac{4^n p_n z^n}{n!^2} = 1 + 12z + 132 z^2 + \ldots
\quad Q(z) = \sum \frac{4^n q_n z^n}{n!^2} = 4z +52 z^2 + \ldots} \)
Then, completely formally, \(DP(z) = 0\) where
\( \displaystyle{ D = z(8z-1)(4z-1) \frac{d^2}{dz^2} + (160 z^2 – 40 z + 1) \frac{d}{dz} + 12(8z – 1)}\)
and \(DQ(z) = 4\). If \(K\) and \(E\) denote the standard elliptic functions, one observes that \(P(z)\) is nothing but the hypergeometric function
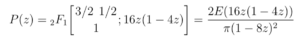
But now one is more or less done! The argument is easily finished with a little help from mathematica. Another solution to \(DF(z) = 0\) is of course
\( \displaystyle{ R(z) = \frac{ 2 E((1-8z)^2) -2 K((1-8z)^2) }{(1 – 8z)^2} = \log(z) + 2 + \ldots } \)
and knowing both homogenous solutions allows one to write \(Q(z) = u(z) P(z) + v(z) R(z)\) and then easily compute that
\(\displaystyle{ \lim_{n \rightarrow \infty} \frac{p_n}{q_n}
= \lim_{z \rightarrow 1/8} \frac{P(z)}{Q(z)} = \frac{2}{-1 + 2G}.}\)
as desired. For those playing at home, note that a convenient choice of \(u(z)\) and \(v(z)\) can be given by
\( \displaystyle{ v(z) = \int \frac{ E(16 z(1-4z))}{\pi} = 4 z – 8 z^2 + \ldots }\)
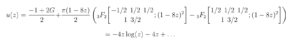

“Here you have to remember that continued fractions, especially of the kind considered in this paper, are more or less equivalent to questions about certain types of ordinary differential equations and their related periods.”
I’d love to understand this statement, where might I start?
Suppose you have a Picard-Fuchs equation over \(\mathbf{P}^1 \setminus \{0,1,\infty\}\) with rational coefficients (so an ODE with coefficients in \(\mathbf{Q}(z)\) . You can expand a basis of solutions around \(0\) as power series (with perhaps some logarithm terms) but with rational coefficients. The coefficients of the holomorphic solutions will satisfy recurrence relations of the form
\(\displaystyle{A_0(n) u_n – A_1(n) u_{n-1} – \ldots – A_k(n) U_{n-k} = 0}\)
for certain polynomials \(A_i(n)\). Given two solutions \(P(z)\) and \(Q(z)\), say, then since \(1\) is a singular point, typically what will happen is that \(P(z) – \alpha Q(z)\) will have better convergence properties for some \(\alpha\) which will imply that the ratio of the coefficients of \(P\) and \(Q\) converge to \(\alpha\). So how to determine \(\alpha\)? Well, you can also find a basis of solutions with rational coefficients in power series expanded around the point \(z = 1\). To determine \(\alpha\), you want to write the rational basis around \(z = 0\) in terms of the rational basis around \(z = 1\), and for a Picard-Fuchs equation you will exactly see the periods arising in this matrix (in particular periods of the degenerate motives in the Picard-Fuchs equations above the singular points).
What is the relation with continued fractions? Well, given any reccurence relation of length \(2\), i.e. \(u_{n} = R(n) u_{n-1} + S(n) u_{n-2}\), then for any two such sequences \(p_n\) and \(q_n\) you can write down a generalized continued fraction out of \(R(n)\) and \(S(n)\) with partial convergents \(p_n/q_n\).
Of course, you can do this even if the original ODE is not of geometric type, but then it is a little less obvious what the change of basis matrix will be, although if you know enough about the solutions to the ODE then this might not be a problem.
And if I understand correctly, you can reverse this process – i.e. given a polynomial continued fraction, find the recurrence satisfied by its convergents, and write down the associated ODE? Then the next step in constructing a proof like the one you have is relating that ODE to ODE’s satisfied by classical special functions (e..g hypergeometrics) and calculating some special values of these functions?
I’m not sure the improved irrationality measures were necessarily part of a failed attempt to prove irrationality. The referee comments are, for some reason, available publicly, and one of the referees specifically suggested that the authors could improve their work by “finding more efficient ways of computing fundamental constants”, without mentioning proving irrationality, and the authors said that they investigated these convergence rate issues in response to that.
Thanks for writing this post for the sake of us poor readers! It was enlightening to me to hear from someone with more expertise in special function wizardry about this (my advisor once told me to read one of the classical books on the subject, which I completely failed to do), and to learn the broader connections between continued fractions and differential equations.
There are of course many wrinkles! One particularly fascinating one is that for Picard-Fuchs equations you can have non-singular points where the Mumford-Tate group of the corresponding Motive changes, and this has implications for the special values of the corresponding solutions to the ODE. The classical manifestation of this is of course the hypergeometric function associated to the Legrendre curve and then specialized at CM points. (This coincidentally comes full circle back to some hypergeometric identities observed by Ramanujan.) For generalized hypergeometric functions this degeneration also happens but more sporadically, because the codimension of the special locus is \(> 1\). But it still happens! See, for example, this paper of Dembélé, Panchiskin, Voight, and Zudilin: https://arxiv.org/abs/1906.07384
(1) Thanks! It makes sense that there are unlikely intersections – I just wanted to know a bit more about what you actually did to find this proof.
(2) I wonder if there is a general framework for, given a particular solution of a particular differential equation, bounding how good of a series of rational approximations you can find by this kind of manipulations. Like, maybe one could show that taking a few fixed identities and multiplying and dividing in arbitrarily complicated ways, we wouldn’t be able to obtain rational approximations strong enough to prove irrationality.
(3) It might be interesting to go through unlikely intersection problems, look for ones where few or no existing examples are known, and then try to find examples by a computer search – hopefully not purely brute force.
(4) One thing I found sociologically interesting is that DZ, who used very similar mathematical ideas to prove some of these formulas, has a diametrically opposite point of view on what that means. It seems that his logic is that if he has a mechanical computer proof of a conjecture or theorem someone came up with by reasoning, that means their work was uninteresting, but if he has a mechanical computer proof of a conjecture someone came up with by computer search, that means their work was interesting.
This is wonderful, is there anywhere I could read a few examples written in full?
It’s worth looking closely at their claims about the algorithms they use.
They put a lot of emphasis on their gradient descent algorithm, saying “We propose a GD optimization method and demonstrate its success in finding RFs. Although proved successful, the MITM-RF method is not trivially scalable. This issue can be targeted by either a more sophisticated variant or by switching to an optimization-based method, as is done by the following algorithm (Fig. 3).” Their response to referee comments includes “It is also the first usage of any gradient descent- type algorithm in this field.”
So how well does this algorithm do? They demonstrate it finding a solution in a sample space of size 2500… The way it works is it picks 500 points in the sample space, and then jiggles the points around until they spread out along local minima, and eventually one of the points hits a solution.
Other than two trivial identities found in tiny parameter spaces, all the other results in the paper are found using the much more conventional “MITM-RF” algorithm.
It’s hard not to see this just as justification for describing their work as “machine learning” and “artificial intelligence” in press releases. Also note Referee 2’s comments suggest they incorrectly thought the gradient descent algorithm was being used for all the results described in the paper. Referee 3 describes the algorithm as “very efficient”.
I personally was surprised that a referee report saying explicitly the paper was not good enough for Nature was not enough to ruin its chances. The referee with negative comments does not seem to have been consulted for the second round. But then, we all know that journals are not perfect in their selection, with both false positives and false negatives all around 🙂