Locally induced representations

Posted on June 16, 2022 by Persiflage

Today is a post about work of my student Chengyang Bao.

Recall that Lehmer’s conjecture asks whether \(\tau(p) \ne 0\) for all primes \(p\), where

\(\Delta = q \prod_{n=1}^{\infty} (1 – q^n)^{24} = \sum \tau(n) q^n\)

is Ramanujan’s modular form. You might recall that Naser Talebizadeh Sardari and I studied a “vertical” version of Lehmer’s conjecture where instead of fixing a modular form, we fixed a prime \(p\) and a tame level \(N\) and showed that there were only finitely many normalized eigenforms \(f\) of level \(N\) and even weight \(k\) with \(a_p(f) = 0\) which were not CM. We exploited the fact that such forms give rise to Galois representations

\(\rho: G_{\mathbf{Q}} \rightarrow \mathrm{GL}_2(\overline{\mathbf{Q}}_p)\)

which are crystalline at \(p\) but also locally induced at \(p\) from the unique unramified quadratic extension \(K/\mathbf{Q}_p\). As explained in this post, it’s hard to see this method being able to say much more to this (for example, to say anything about Lehmer’s actual conjecture), since there do actually exist non-CM forms with \(a_p(f) = 0\).

In practice, we don’t even know in level \(N=1\) whether there exist infinitely many normalized eigenforms \(f\) with \(a_p(f) \equiv 0 \bmod p\). As mentioned in this post, one source of such representations comes from modular forms with exceptional image. For example, if \(f = \Delta E_4\) is the normalized eigenform of weight \(16\), then as first observed by Serre and Swinnerton-Dyer, the mod-\(59\) representation

\(\overline{\rho}_{f}: G_{\mathbf{Q}} \rightarrow \mathrm{GL}_2(\overline{\mathbf{F}}_p)\)

has projective image \(S_4\) coming from the splitting field of \(x^4 – x^3 – 7 x^2 + 11 x + 3\). But the local residual representation in this case is induced, which implies that \(a_{59} \equiv 0 \bmod 59\). As explained in that post, standard conjectures about primes predict that there should be infinitely many \(S_4\)-representations unramified outside a single prime \(p\) giving rise to modular Galois representations which will then come from level one modular forms \(f\) with \(a_p(f) \equiv 0 \bmod p\).

Chengyang’s work concerns examples precisely of this sort. From my work with Naser, we can deduce that there are at most finitely many \(f\) of level one with \(a_{59}(f) = 0\). Chengyang proves that there are no such forms. More precisely:

Theorem [Bao] Suppose that \(f\) is a modular form of level one, and suppose that \(a_p(f) = 0\). Then all of the residual mod-\(p\) representations \(\overline{\rho}\) associated to \(f\) have big image, that is, image containing \(\mathrm{SL}_2(\mathbf{F}_p)\).

In other words, none of the (presumably many) infinite examples of \(S_4\) representations giving rise to \(f\) of level one with \(a_p(f) \equiv 0 \bmod p\) can ever give an \(f\) with \(a_p(f) = 0\).

Chengyang also proves some further results about the deformations of representations with exceptional image. For example, for the mod-\(59\) representation above, the only deformations to characteristic zero unramified outside \(p=59\) which are locally induced are the representations which up to twist are the ones which up to twist coincide with the unique lift with finite image and order prime to \(p=59\).

In contrast, one might ask what happens for \(p=79\), the next case where there exists a form \(f\) of level one with \(a_p(f) \equiv 0 \bmod p\). I suspect that in this case a (possibly quite complicated computation) should show that there should be at most one form with \(a_p(f) = 0\), but that it might be quite difficult to prove using \(p\)-adic methods that there are no such forms. The problem will be that there will exist a deformation which will have infinite image and be locally induced, but now it will have generalized Hodge–Tate weights \([0,\kappa]\) for some \(p\)-adic number \(\kappa\) for which it will be very hard to show is not an integer. This is analogous to the family of Eisenstein series of level one with \(p = 37\). One knows that the \(p\)-adic zeta function will have a unique zero, but it is very hard to probe the arithmetic nature of that zero and to rule out it occurring at some arithmetic weight. To put this slightly differently, is there an integer \(k \ge 1\) such that

\(\zeta_{37}(-31 + 36 k) = 0?\)

Presumably not, but this seems extremely difficult; the difficulty of course is that there will be a solution with \(k \in \mathbf{Z}_{37}\).

Posted in Mathematics, Students, Work of my students | Tagged , , , | 1 Comment

Joël Bellaïche

Posted on June 14, 2022 by Persiflage

Very sad to hear that Joël Bellaïche has just died. He got his PhD at the same time as me, and I first got to know him during the Durham conference in 2004 and later at the eigenvarieties semester at Harvard (was that in 2005 or 2006?).

Joël was an original mathematician, and his papers (many written with Gaëtan Chenevier) contain many really good ideas. As a postdoc, I was totally immersed in thinking about Galois deformations of reducible representations when the paper lisseté de la courbe de Hecke de \(\mathrm{GL}_2\) aux points Eisenstein critiques appeared on the arXiV. In that paper, they study the ideal of reducibility for certain Galois deformation rings (or pseudo-deformation rings). By studying the ring-theoretic properties of this ideal, they proved the Eigencurve was smooth at the evil Eisenstein points. It clarified immediately a number of the phenomena I had been thinking about, but it was also simply the “right” way to think about these things. I also learnt from Joël at Durham the problem of proving the non-vanishing of p-adic zeta values like \(\zeta_p(3) \ne 0\), which remains 18 years later one of my favourite problems.

Another really beautiful idea was the approach by Joël and Gaëtan to Bloch-Kato type conjectures (including the Selmer group part of the Birch–Swinnerton-Dyer conjecture) via the geometry of eigenvarieties (including those associated to \(U(3)\)). This is of course related to the ideal of reducibility. Their joint asterisque paper Families of Galois representations and Selmer groups is a very nice read on this topic, as are Joël’s notes for the Clay summer school as well as his recent book on Eigenvarieties.

In more recent times, Joël had been exploring ideas in some interesting directions, including his intriguing work on self-correspondences on curves. What was consistent about his research was that his primary motivation always seemed to be rooted in coming to an original understanding of interesting math rather than simply making incremental improvements on work of others.

Last but not least, one should not forget his sense of humor with a decidedly irreverent streak. This is probably best appreciated with a beer or a glass of wine in a summer evening in Luminy, but to take a quote from on of Joël’s own papers:

Let \(p\) be a prime number that, we shall assume, splits in \(E\). We shall also assume that \(p \ne 13\). I don’t think this is really useful, but who knows?

My thoughts are with his family.

Posted in Mathematics | Tagged , , , , | 3 Comments

Murphy’s Law for Galois Deformation Rings

Posted on April 23, 2022 by Persiflage

Today’s post is about work of my student Andreea Iorga!

A theorem of Ozaki from 2011, perhaps not as widely known as expected, says the following:

Theorem: Let \(p\) be prime, and let \(G\) be a finite \(p\)-group. Then there exists a number field \(F\) and an extension \(H/F\) such that:

  1. \(H/F\) is the maximal pro-\(p\) extension of \(F\) which is everywhere unramified.
  2. \(\mathrm{Gal}(H/F) = G\).

Since any non-trivial \(p\)-group \(G\) has a non-trivial center, it can be written as a central extension of a smaller \(p\)-group \(G’\) by \(\mathbf{Z}/p \mathbf{Z}\), and thus the proof is (as one might imagine) by induction. The structure of the argument is quite tricky, and it’s a little hard to absorb all the ideas at once. There is a new preprint by Hajir, Maire, and Ramakrishna which gives both a simplification and also an extension of Ozaki’s result (the extension being that one has more explicit control over the degree of \(F\)).

But this post will actually be about a somewhat different generalization due to my student Andreea Iorga (details currently being written up!). Let me give her result now:

Theorem [Iorga] Let \(\Phi\) be a finite group of order prime to \(p\), and let \(G\) be a finite \(p\)-group with an action of \(\Phi\). Assume there exists an extension \(L/K\) such that:

  1. \(L/K\) is Galois with Galois group \(\Phi\),
  2. \(K\) contains \(\zeta_p\),

Then there exists number fields \(H/F/E\) such that:

  1. \(H/F\) is the maximal pro-\(p\) extension of \(F\) which is everywhere unramified.
  2. \(\mathrm{Gal}(H/F) = G\).
  3. \(\mathrm{Gal}(H/E) = \Gamma\), where \(\Gamma\) is the semi-direct product of \(\Phi\) by \(G\) corresponding to the given action of \(\Phi\) on \(G\).

When \(\Phi\) is trivial, one recovers Ozaki’s theorem in the case when \(p\) is a regular prime. In fact, Ozaki’s first proof also has a similar hypothesis. Most likely Iorga’s argument extends to the more general case where one does not need to assume that \(\zeta_p \in E\). (Of course, in order not to accidentally solve the inverse Galois problem, the other two conditions on \(L\) and \(K\) will be necessary!)

One nice consequence (and a motivating example) of Iorga’s theorem is as follows. Consider absolutely irreducible residual representations:

\(\overline{\rho}: G_{K} \rightarrow \mathrm{GL}_2(\mathbf{F}_p)\)

to a finite field. What possible rings \(R\) can occur as deformation rings of all such \(\overline{\rho}\)? In this setting, let \(R\) denote the deformation ring of everywhere unramified representations. Let’s also assume that the image (to be absolutely concrete) has order prime to \(p\), say projectively \(\Phi = A_4\) or \(S_4\). The Fontaine–Mazur conjecture predicts that the only \(\overline{\mathbf{Q}_p}\)-points will have finite image, and thus correspond to the natural lift (assuming the characteristic of \(k\) is \(p \ge 5\)). An argument with class groups then implies that one should expect \(R[1/p] = \mathbf{Q}_p\), or equivalently that \(R\) is a ring admitting a map

\(R \rightarrow \mathbf{Z}_p\)

with finite (as a set) kernel \(I\). A consequence of Iorga’s theorem is the following:

Theorem [Iorga] Let \(R\) be any local ring admitting a surjection to \(\mathbf{Z}_5\) with finite kernel. Then \(R\) is a universal everywhere unramified deformation ring.

This is true for more general regular primes \(p \ge 5\) under the further assumption on the existence of an \(A_4\)-extension of \(\mathbf{Q}(\zeta_p)\) with class number prime to \(p\), the point is that one can find such an extension explicitly for \(p=5\). The key idea to reduce this theorem to the previous one is a follows. Suppose that the image of \(\overline{\rho}\) is \(\widetilde{\Phi}\). Since this has order prime to \(p\), it lifts to a representation \(\widetilde{\Phi} \subset \mathrm{GL}_2(\mathbf{Z}_p)\). Then let \(\Gamma\) denote the inverse image of this group inside \(\mathrm{GL}_2(R)\), so it lives inside an exact (split) sequence:

\( 1 \rightarrow 1 + M_2(I) \rightarrow \Gamma \rightarrow \widetilde{\Phi} \rightarrow 1\)

The group \(\Gamma\) admits a natural residual representation via \(\overline{\rho}\), and clearly \(\Gamma\) admits a deformation to \(\mathrm{GL}_2(R)\) by construction. The point is that one can show that this \(R\) is the universal deformation ring, and hence providing one has extensions \(H/F/E\) with \(\mathrm{Gal}(H/E) = \Gamma\) and \(H/F\) the maximal everywhere unramified pro-\(p\) extension of \(F\) (using the previous theorem) one is in good shape. (There is a trick to reduce the problem in this case to \(\Phi\) in order to make the “base case” easier, since one has fields \(F/\mathbf{Q}\) and \(\widetilde{F}/\mathbf{Q}\) with \(\mathrm{Gal}(F/\mathbf{Q}) = \Phi\) and \(\mathrm{Gal}(\widetilde{F}/\mathbf{Q}) = \widetilde{\Phi}\) and if \(\Phi = A_4\) and \(p = 5\) then proving that \(F(\zeta_5)\) of degree \(48\) has class number prime to \(5\) is easier than the same claim for \(\widetilde{F}(\zeta_5)\) of degree some multiple of \(96\)).

One way to view this result is as an example of “Murphy’s Law” for moduli spaces. This is the idea explained by Ravi Vakil that all possible singularities occur inside deformation spaces (of a more geometric kind rather than Galois deformation rings). The analogue in the setting of Galois deformation rings is to say that all possible local rings (subject to some obvious constraints) occur as Galois deformation rings. Still considering the case of everywhere unramified deformation rings, another natural class of rings one might expect to arise in this way is the set of all finite artinian local rings. Of course for such rings one would have to consider residual representations whose images have order divisible by \(p\), requiring a further modification of the theorems of Ozaki and Iorga. In a different direction, one can ask what happens for deformation conditions with other local conditions at \(p\). Here are two natural such questions:

Problem Let \((R,\mathfrak{m})\) be any complete local Noetherian ring with finite residue field which is finite over \(W(k)\). Then does \(R\) occur as the finite flat deformation ring of some absolutely irreducible residual representation?

Problem Let \((R,\mathfrak{m})\) be any complete local Noetherian ring with finite residue field over \(W(k)\), and assume that:

  1. \(R\) is a complete intersection, namely that there is a presentation:
    \(R \simeq W(k)[[x_1,\ldots,x_d]]/(f_1,\ldots,f_r)\)
    where \(d \ge r\).
  2. \(p \in R\) is a regular element.

Then does \(R\) occur as the universal deformation ring (with fixed determinant) of some
absolutely irreducible residual representation? Note that the conditions given are both conjectured (but unknown in general) to be necessary conditions in this case.

I would guess the first problem has a positive answer but I’m honestly not even sure about the second one! This is already very interesting in the case (say) of a totally even representation with the addtional requirement that \(r = d\).

Update: A friend of the blog points out that the second problem most likely falls prey to countability issues when \(R\) is not finite over \(W(k)\) and indeed that seems to be an issue. I’m not quite sure what the optimal modified version should be; perhaps one could ask that for any \(k\) there are a deformation rings \((S,\mathfrak{m}_S)\) such that \(R/\mathfrak{m}^k = S/\mathfrak{m}^k_S\), perhaps even insisting that \(S\) is a complete intersection of the same dimension as \(R\) as well. The case when \(r=d\) still might be OK

Posted in Mathematics, Students, Work of my students | Tagged , , , , , , , , | 11 Comments

What would Deuring do?

Posted on April 13, 2022 by Persiflage

This is an incredibly lazy post, but why not!

Matt is running a seminar this quarter on the Weil conjectures. It came up that one possible way to prove the Weil conjectures for elliptic curves over finite fields is to lift them to CM elliptic curves using Deuring’s theorem. But after some discussions we couldn’t quite work out whether this was circular or not.

Certainly if you can lift to a CM elliptic curve and lift Frobenius to an endomorphism \(\phi\) of the lift you get Weil immediately; the degree of \(\phi\) is \(p\) which implies the norm of \(\phi\) is \(p\), but for imaginary quadratic fields the norm coincides with the absolute value. But how did Deuring prove his theorem?

The most obvious way to lift an (ordinary, say) elliptic curve \(E/\mathbf{F}_p\) to characteristic zero is to note that, by the Weil conjectures, the order \(\mathcal{O} = \mathbf{Z}[\phi]\) generated by Frobenius lies inside an imaginary quadratic field \(K\) (this is equivalent to the Weil conjectures), and so one can consider \(\mathbf{C}/\mathbf{Z}[\phi]\). To make things simple, if the order is maximal, then this is defined over the Hilbert class field \(H\) of \(K\), and since \(p\) splits principally in \(K\) (since \(\phi\) has norm \(p\)) it follows that \(p\) splits principally in \(H\) as well by class field theory, and so the CM elliptic curve is also defined over \(\mathbf{Z}_p\) and gives a lift. Of course, this argument uses the Weil conjectures! Without that, the ring \(\mathcal{O}\) lives inside a real quadratic field and it’s not clear what one can do.

One approach is to prove the existence of the canonical lift, which automatically will have extra endomorphisms and thus be CM since it lives in characteristic zero. This doesn’t depend on the Weil conjectures. But the canonical lift is a construction I associate more with Serre-Tate than with Deuring. But it’s certainly possible that Deuring’s argument was via the canonical lift.

Some might say that the easy way to solve this is simply to look in one of Deuring’s papers. But instead I will try to call upon my readers (possibly either number theorists who speak German or Brian Conrad) to save me the work and tell reveal all in the comments!

Posted in Mathematics | Tagged , , , , , | 3 Comments

A random curve over Q

Posted on April 2, 2022 by Persiflage

Let \(X/\mathbf{Q}\) be a smooth projective curve. I would like to be able to say that the motive \(M\) associated to \(X\) “generally” determines \(X\). That is, I would like to say it in a talk without feeling like I’m telling too much of a fib. But is this true? There are two issues. Recall that, by the Torelli Theorem, the Jacobian together with a principle polarization determines \(X/\mathbf{C}\). So there are two things to worry about:

  1. Knowing \(M\) only recovers the Jacobian up to isogeny, and you can certainly have two different curves with isogenous Jacobians, even isomorphic Jacobians with different polarizations.
  2. Knowing \(X/\mathbf{C}\) does not determine \(X/\mathbf{Q}\).

To overcome the second issue, it is sufficient and necessary to assume that \(\mathrm{Aut}_{\mathbf{C}}(X)\) is trivial. Let me ignore the first point, since I both assume it generically doesn’t happen but since I can’t even address the second point yet I haven’t thought about it yet.

Perhaps this is obvious to a geometer, but I don’t see why a “random” curve \(X/\mathbf{Q}\) doesn’t have automorphims. My model of a random curve is to take, for example, an embedding of \(M_g\) into projective space and then count points by the ambient height function and see what ratio of points has trivial automorphisms. (Presumably any other counting function like Faltings height or whatever will more or less be the same.) Certainly a generic \(\mathbf{C}\)-point of \(M_g\) has no automorphisms (at least for \(g > 2\)), but since \(M_g\) is of general type for large enough \(g\) I don’t whether one can find enough rational points which are generic!

Probably the most natural way to answer this is to give a positive answer to the following question:

Question: Does \(M_g\) contain a subvariety \(X\) which is unirational over \(\mathbf{Q}\) and has dimension strictly greater than the hyperelliptic locus?

Or, to put it more naturally, can you just explicitly write down enough generic curves which don’t have any automorphisms to see that they dominate any point count?

Posted in Mathematics | Tagged , , | 16 Comments

ArXiv x 3

Posted on March 4, 2022 by Persiflage

Three recent arXiv preprints this week caught my interest and seemed worth mentioning here.

The first is a paper by Oscar Randal-Williams, which considers (among other things) the cohomology of congruence subgroups of \(\mathrm{SL}_N(\mathbf{Z})\) in the stable range. This is definitely something I have talked on the blog about a number of times, including here and here. To recall; Matthew Emerton and I proved that the completed cohomology groups

\(\widetilde{H}^d(\mathbf{F}_p) = \lim H^d(\mathrm{SL}_N(\mathbf{Z},p^n),\mathbf{F}_p)\)

are independent of \(N\) for \(N\) sufficiently large with respect to \(d\), and are moreover finite vector spaces with a trivial action of \(G = \mathrm{SL}_N(\mathbf{Z}_p)\). I later explained moreover how these groups are the cohomology groups of the homotopy fibre of the map from \(\mathrm{SK}(\mathbf{Z};\mathbf{Z}_p)\) to \(\mathrm{SK}(\mathbf{Z}_p;\mathbf{Z}_p)\). But now the Quillen-Lichtenbaum conjecture shows (thanks to Blumberg and Mandell) how the homotopy groups of these spaces are identified with Galois cohomology groups, which allows one to compute the maps between homotopy groups and understand (at the very least) the cohomology groups in degrees less than \(p\). Since one has a Hochschild-Serre spectral sequence

\(E^{i,j}_2 = H^i(G(p),\widetilde{H}^j(\mathbf{F}_p)) \Rightarrow H^{i+j}(\mathrm{SL}(\mathbf{Z},p),\mathbf{F}_p),\)

this allows one to compute the cohomology of \(\mathrm{SL}(\mathbf{Z},p)\) over \(\mathbf{F}_p\) in low degree by analyzing this spectral sequence. I later came to suspect that for regular primes \(p\) this spectral sequence degenerated immediately at least in degrees less than \(p\) or so, which would allow one to compute the cohomology groups in degree \(d\) explicitly for all large regular \(p\). Actually the prediction was slightly stronger: in the range of cohomology degrees at most \(d\) one only had to avoid a finite set of primes (those dividing \(B_{2k}\) for small \(k\) together with the set of primes \(p\) which divided the finitely many zeta values \(\zeta_p(3), \zeta_p(5), \ldots \zeta_p(2k+1)\) also for small \(k\)). Oscar not only proves this but goes one step further, by showing that it degenerates in small degrees for any prime \(p\), even as a \(\mathrm{SL}(\mathbf{F}_p)\)-module. This implies, for example, that, with \(H^1(G(p),\mathbf{F}_p) = M\) being more or less the adjoint representation, that

\(H^4(\mathrm{SL}_N(\mathbf{Z},p),\mathbf{F}_p) = \mathbf{F}_p \oplus \wedge^2 M \oplus \wedge^4 M\)

for \(p > 5\) if and only if \(p\) does not divide the \(p\)-adic zeta function \(\zeta_p(3)\), and

\(H^4(\mathrm{SL}_N(\mathbf{Z},p),\mathbf{F}_p) = \mathbf{F}_p \oplus \mathbf{F}_p \oplus \wedge^2 M \oplus \wedge^4 M\)

otherwise. Note this condition implies that \(p\) is irregular but is much more restrictive. But it does actually happen! The only known primes with this property are \(p = 16843\) and \(p=2124679\).

Part of my original interest in this problem came from Benson Farb and Tom Church — they noted that these groups should be stable in the weaker sense that they should be “independent of \(N\)” more or less exactly in the sense that there is a uniform description as above (proved later by Andrew Putman), but this left open the question of what the groups actually were. Of course my feeling is that the completed cohomology groups are more “fundamental” and the cohomology at finite level is really just a frothy mix of unwinding what happens in the limit, but one has to admit that this new result is pretty satisfying.

————————

The second is a paper by Will Sawin and Melanie Wood. I remember 20 years ago or so being one of three BPs at Harvard asked to give a small presentation to the Harvard “Friends of Math” (Will Hearst and the gang), along with William Stein and Nathan Dunfield. One memory was that my talk was a chalk talk and theirs were both involved much snazzier technology. But I also remember that Nathan talked about his very nice paper with Bill Thurston on random 3-manifolds. In Melanie and Will’s new paper, they beautifully exploit many of the recent progress on “random groups” (much of it due to the authors themselves) to show that the profinite completion of a random 3-manifold (in the sense of a random Heegaard splitting for larger and larger genus) itself has a limiting distribution.

Here is just one immediate corollary of their results which ties into previous problems considered both by Nathan and me and also Nigel Boston and Jordan Ellenberg. (Actually I say corollary, but I am just guessing that this should easily be a corollary without actually doing any of the computation so any error here is due to me!)

Expected Corollary: For a fixed prime \(p > 2\) and a “random” 3-manifold \(M\), there is a positive probability that:

1. There is a surjection: \(\pi_1(M) \rightarrow \mathrm{SL}_2(\mathbf{Z}_p)\),
2. The corresponding tower of covers \(M_n\) coming from congruence subgroups all have trivial first Betti number.

The point of course being that (as in Boston-Ellenberg) one can deduce this from the more restrictive condition that the kernel \(N\) of the map

\(\pi_1(M) \rightarrow \mathrm{SL}_2(\mathbf{F}_p)\)

has \(N/N^p = (\mathbf{F}_p)^3\) and no larger, and hence it can be phrased as the pro-finite completion of \(\pi_1(M)\) surjecting onto one pro-finite group but not some other finite group. (Here \(N/N^p = (\mathbf{F}_p)^3\) can I think be weakened to \(N/N^p[N,N] = (\mathbf{F}_p)^3\) by an argument of Simon Marshall). I guess another way of saying this is that the pro-p completion of the cover \(N\) can be described explicitly as the \(p\)-congruence subgroup of \(\mathrm{SL}_2(\mathbf{Z}_p)\).

Of course, this work also raises the very natural question:

Question: What is the distribution of \(\widehat{\pi_1(M)}\) on arithmetic 3-manifolds? What about congruence arithmetic 3-manifolds?

The main point of course is that the existence of Hecke operators imposes a lot of extra structure, which one certainly expects (and can be numerically observed) changes the distribution of any given finite group occurring. Here I think the sensible question is to ask for a conjecture rather than a theorem, of course! (Maybe the first sensible question is actually to give a good conjecture for the distribution of the abelianization of these groups…)

————————

The last paper is this one by Peter Kravchuk, Dalimil Mazáč, and Sridip Pal, which I am even less qualified to talk about, which gives remarkable upper bounds for the smallest Laplacian eigenvalue of a (closed) hyperbolic orbifold of fixed genus. For example, when \(g = 2\), they give the bound \(\lambda_1 < 3.8388976481\), which is not too shabby given that there is an example with \(\lambda_1 = 3.83888725\ldots\)! The paper has a number of other gems, including more or less identifying the complete spectrum of all \(\lambda_1\) as comprising a set of isolated points combined with the entire interval \([0,\alpha]\) for some \(\alpha = 15.8\ldots\).

Posted in Uncategorized | Tagged , , , , , , , , , , , , , , , , , , | 2 Comments

What would a good ICM talk look like?

Posted on February 27, 2022 by Persiflage

Now that the ICM has (unsurprisingly) become a virtual event, it might be worthwhile thinking a little bit about what would constitute a good talk in this new setting. There’s a certain electricity to talks given in person, and I think that many speakers give better talks when they have an opportunity to read the audience. Certainly the zoom talks I have most enjoyed watching are those where I’ve been able to interact with the speaker, but that clearly becomes impossible once the audience is large enough.

So an ICM of zoom talks (on a St Petersburg schedule in the middle of the night in Chicago) does sound a little uninspiring. But what would be better? pre-recorded zoom lectures sound even worse. The idea of a polished video presentation has some appeal, but possibly it is also unrealistic. The sound and audio quality of a standard zoom lecture are OK if you are interested enough in the material, but I think one should expect a general ICM audience to be a little less forgiving. (Yes, plenty of people give terrible colloquia, but at least there are usually cookies.) And even with access to high quality audio and video, is it just going to be someone standing in front of their blackboard?

I have tried once to make a mathematics video which was something other than me giving a lecture, and honestly, it took me a lot of time and didn’t turn out that great. But as Tim Gowers says on Terry’s blog, this should at least be an opportunity for speakers to try something.

Any thoughts? I guess the speakers have a few months to come up with some ideas!

Posted in Mathematics, Politics | Tagged , , , , | 3 Comments

Boxes for Boxer

Posted on January 4, 2022 by Persiflage

My brother texted me on Monday saying that there were seven (or so) boxes pilled up (outside!) in front of the mathematics department and all addressed to George Boxer. My first thought was that this was a transatlantic move gone horribly wrong, so I emailed the department looking for volunteer graduate students to haul the boxes inside. I managed to acquire the boxes the next day:

Boxes

Now the boxes turned out not to contain the entire sum of George’s possessions (nor a large pile of cash, unfortunately), but somewhat more hilariously it consisted of reprints from our recently published paper (previously blogged about here). This was amazingly silly for a number of reasons. First, at 350 pages, the paper is kind of bulky, and certainly AFAIK nobody asked for reprints. Second, George Boxer hasn’t been at Chicago for a few years (though admittedly that is his listed address on the paper). Third, if IHES is going to send 17,500 pages of math to one of the four authors, perhaps it might have made more sense to send it to Vincent Pilloni who is five minutes away from IHES rather than to Chicago? Looking more closely at the boxes it seems as though the big boxes contain eight copies of the paper and the one small box contained two. But actually there were only 5 big boxes rather than six, so only 42 copies in total rather than 50. That makes me suspect that one of the boxes went missing. Possibly a porch pirate ran off with a box before they were carried inside (look for copies on the black market at 57th street books), or maybe there is a box floating in the Atlantic somewhere… Anyway, I now have a large collection of bulky (but still surprisingly light — perhaps recycled paper) reprints in my office. I think it should make good fort building material for LC.

Fort Building Material

Posted in Mathematics | Tagged , , , , | 6 Comments

Simons Annual Meeting

Posted on December 23, 2021 by Persiflage

The last time I traveled for math was when I gave the Coble lectures at UIUC pre-pandemic (at least pre-pandemic as far as the US goes). A few months ago it seemed like one could begin to start traveling again, so I agreed to go to the Simons Conference scheduled for Jan 13-14 in NYC. While I’m prepared as the next person to acknowledge that we have to start living with the coronavirus and live our lives accordingly, traveling during might be the absolute peak of omicron in NYC seems a little unwise. Hence I sadly cancelled my trip today. I was hoping to get a chance to chat with people about Mumford 4-folds, and I had already decided on going to Rezdôra for a pasta tasting menu plus wine tasting menu. But it is not to be. It’s honestly quite surprising to me that many other people seem very happy to go to the same meeting. I can’t quite tell if they have a higher tolerance for risk or if one of us (or both) are simply not estimating the risk accurately. If it goes ahead, I hope it goes well for everyone there!

Update: Cancelled!

Posted in Mathematics, Travel | 3 Comments

Schur-Siegel-Smyth-Serre-Smith

Posted on November 25, 2021 by Persiflage

If \(\alpha\) is an algebraic number, the normlized trace of \(\alpha\) is defined to be

\( \displaystyle{T(\alpha):=\frac{\mathrm{Tr}(\alpha)}{[\mathbf{Q}(\alpha):\mathbf{Q}].}}\)

If \(\alpha\) is an algebraic integer that is totally positive, then the normalized trace is at least one. This follows from the AM-GM inequality, since the normalized trace is at least the \(n\)th root of the norm, and the norm of a non-zero integer is at least one. But it turns out that one can do better, as long as one excludes the special case \(\alpha = 1\). One reason you might suspect this to be true is as follows. The AM-GM inequality is strict only when all the terms are equal. Hence the normalized trace will be close to one only when many of the conjugates of \(\alpha\) are themselves close together. But the conjugates of algebraic integers have a tendency to repel one another since the product of their differences (the discriminant is also a non-zero integer.) In an Annals paper from 1945, Siegel (bulding on a previous inequality of Schur) proved the following:

Theorem [Siegel] There are only finitely many algebraic integers with \(T(\alpha) < \lambda\) for \(\lambda = 1.7336105 \ldots\)

Siegel was also able to find that the only such integers with noramlized trace at most \(3/2\) are \(1\) and \((3 \pm \sqrt{5})/2 = \phi^{\pm 2}\) for the golden ratio \(\phi\) (We will also prove this below). On the other hand (generalizing these examples), one has

\(\displaystyle{T(\left((\zeta_p + \zeta^{-1}_p)^2\right) = 2 \left(1 – \frac{1}{p-1} \right),}\)

and hence the optimal value of \(\lambda\) is at most \(2\). Sometime later, Smyth had a very nice idea to extend the result of Siegel. (An early paper with these ideas can be found here.) Consider a collection of polynomials \(P_i(x)\) with integral coefficients, and suppose that

\(Q(x) = -\lambda + x \ – \sum a_i \log |P_i(x)| \ge 0\)

for all real positive \(x\) where \(Q(x)\) is well-defined, and where the coefficients \(a_i\) are also real and non-negative. Now take the sum of \(Q(x)\) as \(x\) ranges over all conjugates of \(\alpha\). The key point is that the sum of \(\log |P_i(\sigma \alpha)|\) is log of the absolute value of the norm of \(P_i(\alpha)\). Assuming that \(\alpha\) is not a root of this polynomial, it follows that the norm is at least one, and so the log of the norm is non-negative, and so the contribution to the sum (since \(-a_i\) is negative) is zero or negative. On the other hand, after we divide by the degree, the sum of \(\lambda\) is just \(\lambda\) and the sum of \(\sigma \alpha\) is the normalized trace. Hence one deduces that \(T(\alpha) \ge \lambda\) unless \(\alpha\) is actually a root of the polynomial \(P_i(x)\). So the strategy is to first find a bunch of polynomials with small normalized traces, and then to see if one can construct for a constant \(\lambda\) as close to \(2\) as possible some function \(Q(x)\) which is always positive.

One can make this very explicit. Suppose that

\(\displaystyle{Q(x) = -\lambda + x – \frac{43}{50} \cdot \log |x| – \frac{18}{25} \cdot \log |x-1| – \frac{7}{50} \cdot \log|x-2|,}\)

Calculus Exercise: Show that, with \(\lambda = 1.488753\ldots\), that \(Q(x) \ge 0\) for all \(x\) where it is defined. Deduce that the only totally real algebraic integer with \(T(\alpha) \le \lambda\) is \(\alpha = 1\). The graph is as follows:

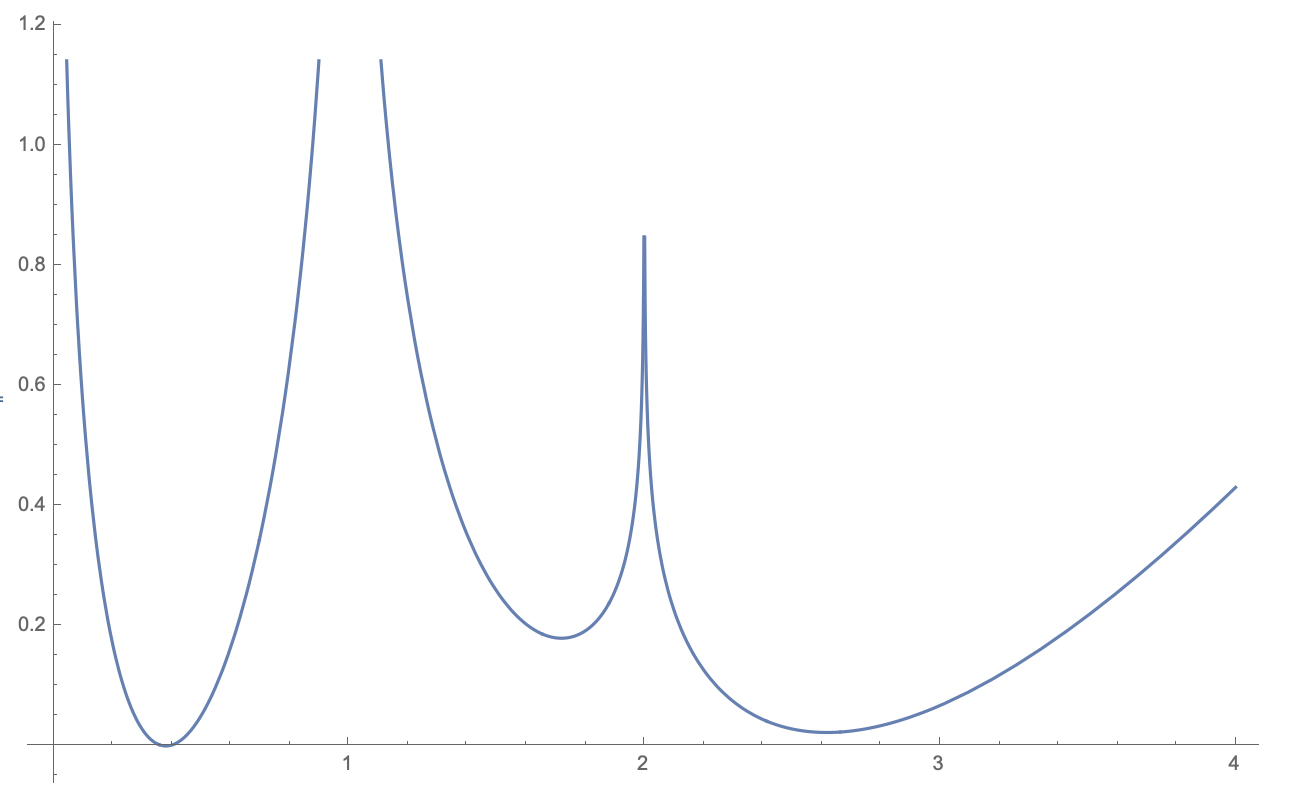
a positive function

One can improve this by increasing \(\lambda\) and modifying the coefficients slightly, but note that we can’t possibly modify this with the given polynomials to get \(\lambda> 3/2\), because \(T(\phi^2) = 3/2\). Somewhat surprisingly, we can massage the coefficients reprove the theorem of Siegel and push this bound to \(3/2\). Namely, take

\(\displaystyle{Q(x) = -\frac{3}{2} + x – a \log |x| – (2a-1) \log |x-1| – (1-a) \log|x-2|,}\)

and note that the derivative satisfies

\(Q'(x)x(x-1)(x-2) = (x^2-3x+1)(x-2a),\)

Hence the minimum occurs at either \(x=2a\) or at the conjugates of \(\phi^2\) where \(\phi\) is the golden ratio. Since \(\phi^2-1 = \phi\) and \(\phi^2-2 = \phi^{-1}\), one finds that

\(Q(\phi^2) = -\frac{3}{2} + \phi^2 + (2-5 a) \log \phi,\)

and so chosing \(a\) so that this vanishes when, we get

\(\displaystyle{a = \frac{2}{5} + \frac{1}{2 \sqrt{5} \log \phi} = 0.864674\ldots} \)

and then we find that \(Q(x) \ge 0\) for all \(x\) where it is defined with equality at \(\phi^2\) and \(\phi^{-2}\). So this reproves Siegel’s theorem by elementary calculus. Of course we can strictly improve upon this result by including the polynomial \(x^2 -3x + 1\), for example, replacing \(Q(x)\) by
.
\(\displaystyle{P(x) = Q(x) – \frac{1}{15} \cdot \log |x^2 – 3x + 1| + \left(\frac{3}{2} – \lambda\right)}\)

where \(\lambda = 1.5444\ldots \) is now strictly greater than \(3/2\). By choosing enough polynomials and optimizing the coefficients by hook or crook, Smyth beat Siegel’s value of \(\lambda\) (even with an explicit list of exceptions), although he did not push \(\lambda\) all the way to \(2\). This left open the following problem: is \(2\) the first limit point? That is, does Siegel’s theorem hold for any \(\lambda < 2\)? This was already asked by Siegel and it became known as the Schur-Siegel-Smyth problem. Some point later, Serre made a very interesting observation about Smyth's argument. (Serre's original remarks were in some letter which was hard to track down, but a more recent exposition of these ideas is contained in this Bourbaki seminar.) He more or less proved that Smyth’s ideal could never prove that \(2\) was the first limit point. Serre basically observed that there existed a measure \(\mu\) on the positive real line (compactly supported) such that

\(\int \log |P(x)| d \mu \ge 0\)

for every polynomial \(P(x)\) with integer coefficients, and yet with

\(\int x d \mu = \lambda < 2\)

for some \(\lambda \sim 1.89\ldots \). Since Smyth’s method only used the positivity of these integrals as an ingredient, this means the optimal inequality one could obtain by these methods is bounded above by Serre’s \(\lambda\). On the other hand, Serre’s result certainly doesn’t imply that the first limit point of normalized traces of totally positive algebraic integers is less than \(2\). A polynomial with roots chosen uniformly from \(\mu\) will have normalized trace close to \(\lambda\), but it is not at all clear that one can deform the polynomial to have integral coefficients and still have roots that are all positive and real.

I for one felt that Serre’s construction pointed to a limitation of Smyth’s method. Take the example of \(Q(x)\) we considered above. We were able to prove the result for \(\lambda = 3/2\) by virtue of the fact that \(Q(x)=0\) at these points. But that required the fact that the three quantities:

\(\phi^2, \phi^2 -1 = \phi, \phi^2- 2 = \phi^{-1}\)

were all units and so of norm one. The more and more polynomials one inputs into Smyth’s method, the inequalities are optimal only when \(P_i(\alpha)\) is a unit for all the polynomials \(P_i\). But maybe there are arithmetic reasons why non-Chebychev polynomials (suitably shifted and normalized) must be far from being a unit when evaluated at \((\zeta + \zeta^{-1})^2\) for a root of unity \(\zeta\).

However, it turns out my intuition was completely wrong! Alex Smith has just proved that, for a measure \(\mu\) on (say) a compact subset of \(\mathbf{R}\) with countably many components and capacitance greater than one, that if Serre’s (necessary) inequality

\( \int \mathrm{log}|Q(x)| d \mu \ge 0\)

holds for every integer polynomial \(Q(x)\), then you can indeed find a sequence of polynomials with integer coefficients whose associated atomic measure is weakly converging to \(\mu\). In particular, this shows that Serre’s example actually proves the maximal \(\lambda\) in the Schur-Siegel-Smyth problem is strictly less than \(2\), and indeed is probably equal to something around \(1.81\) or so. Remarkable! I generally feel that my number theory intuition is pretty good, so I am always really excited when I am proved wrong, and this result is no exception.

Exercise for the reader: One minor consequence of Smith’s argument is that for any constant \(\varepsilon > 0\), there exist non-Chebyshev polynomials \(P(x) \in \mathbf{Z}[x]\) such that, for primes \(p\) say and primitive roots of unity \(\zeta\), one has

\( \displaystyle{\log \left| N_{\mathbf{Q}(\zeta)/\mathbf{Q}} P(\zeta + \zeta^{-1}) \right|} < \varepsilon [\mathbf{Q}(\zeta_p):\mathbf{Q}]\)

for all sufficiently large primes \(p\). Here by non-Chebyschev I mean to rule out “trivial” examples that one should think of as coming from circular units, for example with \(P(\zeta + \zeta^{-1}) = \zeta^k + \zeta^{-k}\) for some fixed \(k\). Is there any other immediate construction of such polynomials? For that matter, what are the best known bounds for the (normalized) norm of an element in \(\mathbf{Z}(\zeta)\) which is not equal to \(1\), and ruling out bounds of elements in the group generated by units and Galois conjugates of \(1-\zeta\)? I guess one expects the class number \(h^{+}\) of the totally real subfield field to be quite small, perhaps even \(1\) infinitely often. Then, assuming GRH, there should exist primes which split completely of order some bounded power of \(\log |\Delta_K|\), which gives an element of very small norm (bounded by some power of \([\mathbf{Q}(\zeta):\mathbf{Q}]\)). However, this both uses many conjectures and doesn’t come from a fixed polynomial. In the opposite direction, the most trivial example is to take the element \(2\) which has normalized norm \(2\), but I wonder if there is an easy improvement on that bound. There is an entire circle of questions here that seems interesting but may well have easy answers.

Posted in Mathematics | Tagged , , , , , | 5 Comments