Deciphering Quanta

Posted on March 23, 2023 by Persiflage

Sometimes it is claimed that Quanta articles are so watered down of mathematical content that they become meaningless. That presents a challenge: do I understand the quanta article on my own work?

Here goes:

New Proof Distinguishes Mysterious and Powerful ‘Modular Forms’

I can confirm that I did not see this article in any form before it appeared. Overall I would say that it is faithful to the facts and I can interpret what everything means. I’m not quite sure why there is an Alex Kontorovich explainer about the Langlands Program in there but why not?

I did, however, have to stop and wonder when I saw the following picture:

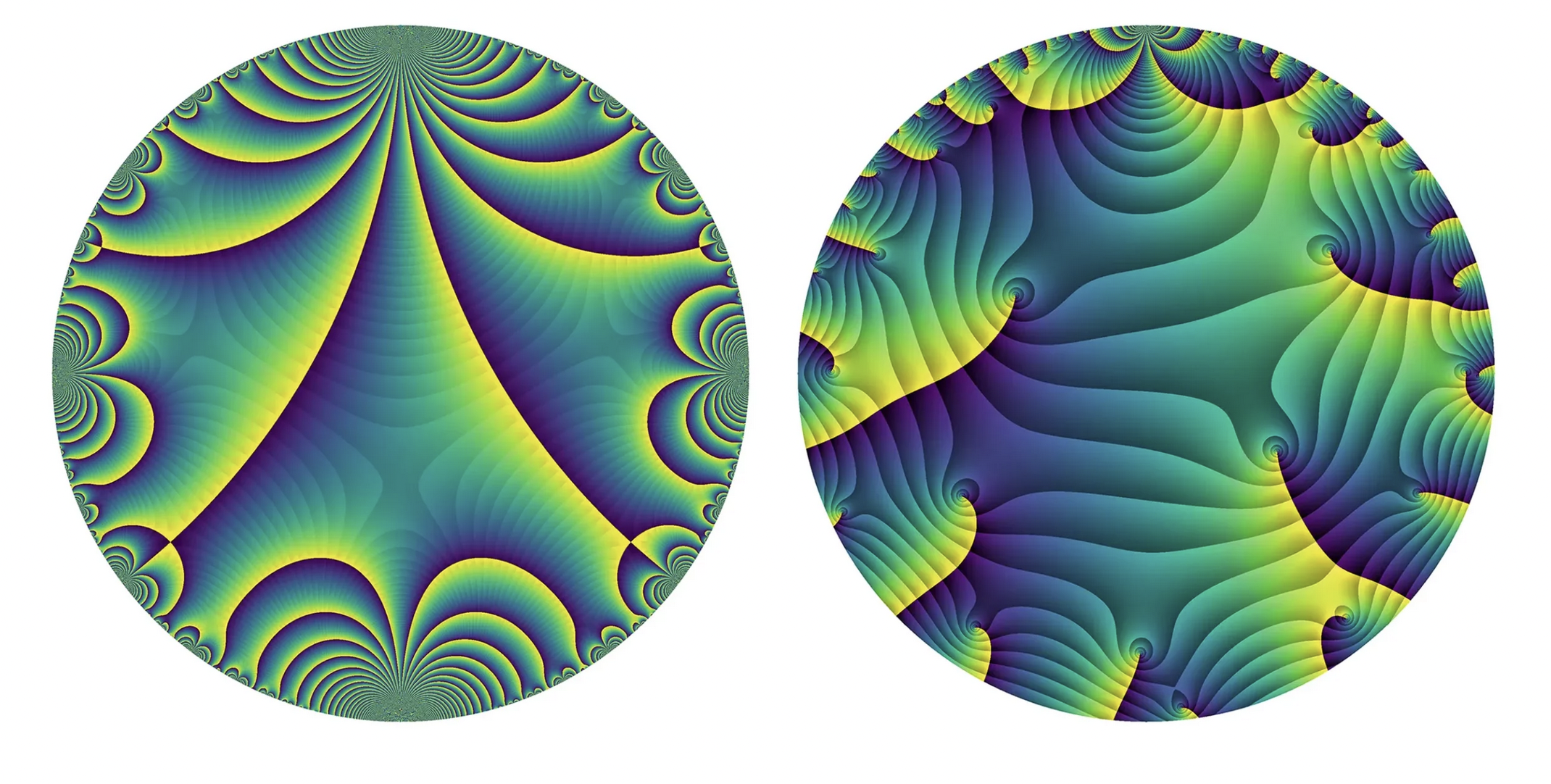
This appeared with the caption *Congruence modular forms (left) have additional structure that noncongruence modular forms (right) lack.* OK, here is the challenge: can I work out what this picture actually represents?

In both pictures, there is clearly some color gradient between yellow and blue, and this has discontinuities along some regions we call \(L\) and \(R\) for left and right. These are also clearly pictures inside \(\mathbf{H}^2\) in the Poincaré disc model.

Here \(L\) looks at least superficially like a fundamental domain for some Fuchsian group. The rays of \(L\) going towards the point \(i\) on the boundary do look like geodesics in the hyperbolic metric (which are circular arcs meeting the boundary at right angles). There is a corresponding invariance for the figure by the parabolic element (with some cusp width) through \(i\). Consider a conformal map from the upper half plane to this model which sends \(\infty\) to \(i\):

Using the standard conformal map with the upper half plane:

\(\phi: \mathbf{H} \rightarrow D(0,1), \quad z \mapsto \displaystyle{\frac{1 + i z}{1 + z}} \)

From the picture, we see the images of the geodesics from the infinite cusp to \(n \alpha\) for \(n\) odd. All parabolic elements are conjugate, but if we are to guess what \(\Gamma\) is by looking at the picture then working out \(\alpha\) for this specific model is important. I tried to eyeball it for a while before printing it out and trying to compute the angle using continued fractions, which wasn’t so accurate but gave \(\tan \theta \sim 1/(1 + 1/3)\) with \(\theta\) in the mid \(30\)s. Then using some angle tools in keynote it came out to somewhere between \(36\) and \(37\) degrees, closer to the latter. So maybe it was exactly a \(10\)th root of unity, which would make \(\alpha\) live in a degree \(4\) field, or (much better!) maybe \(\alpha = 1/2\) in which case the angle is \(36.8698 \ldots\), and then \(L\) (or rather \(\phi(L)\) is invariant under exactly

\(A = \left( \begin{matrix} 1 & 1 \\ 0 & 1 \end{matrix} \right).\)

Maybe I should have guessed this in retrospect! Let’s look at the geodesic from \(i \infty\) to \(1/2\), which in the picture goes from \(i\) to \(4/5 – 3i/5\). There appears to be a point with \(4\)-fold symmetry. That suggests invariance under some order four element corresponding to an elliptic point. But this is a little worrying, since \(\mathrm{PSL}_2(\mathbf{Z})\) does not have any elements of order \(4\)! Now there are some ways around this. For example, this could be the level set of a function which satisfies an extra invariance property under the normalizer of some congruence subgroup, and so does not itself come from an element of \(\mathrm{SL}_2(\mathbf{Z})\) but \(\mathrm{GL}_2(\mathbf{Q})^{+}\). For example, the Fricke involution on \(X_0(N)\) is \(\tau \mapsto -1/N \tau\) which corresponds to. a matrix in \(\mathrm{GL}_2({\mathbf{Q}})\) with determinant \(N\), although that has order \(2\). Any element of order \(4\) has to have eigenvalues of the form \(\alpha\) and \(\alpha i\), with \(\alpha + i \alpha \in {\mathbf{Z}}\), and thus eigenvalues \(1+i\) and \(1-i\) up to rational multiples. That means the determinant should be \(2\) times a square. The unique element such element up to conjugacy is

\(S = \left( \begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix} \right)\)

which has order \(4\) and fixes \(i\). If we want to fix a point on the geodesic \(1/2 + i t\), we can just make a hyperbolic scaling and then conjugate to get the matrix

\(S_t = \left( \displaystyle{ \begin{matrix}
1 – 1/2t & t + 1/4t \\
-1/t & 1 + 1/2t \end{matrix} } \right).\)

Here I started to run into a problem because it’s hard to approximate \(t\) to any precision from the picture, although \(t \sim 0.1\) numerically. There are a few natural integral matrices one can write down but it wasn’t clear what was going on.

Next I turned to the picture around the cusp \(-i\). This looks kind of weird because the biggest curves decidedly do not look like geodesics. But if we ignore this, we might decide that \(-i\) is another cusp. It’s also disturbing that the fundamental domain appears to contain enough of the boundary to suggest that \(\Gamma\) is a thin group, but let’s ignore this as well. So what is the cusp width (with out normalizations) at \(-i\)? Here numerically I simply get nonsense.because if there really were geodesics around \(i\) translated by a fixed parabolic element and the first one was of the size indicated in the picture then there would be many fewer visible ones. As a typical example, one should expect a picture like this:

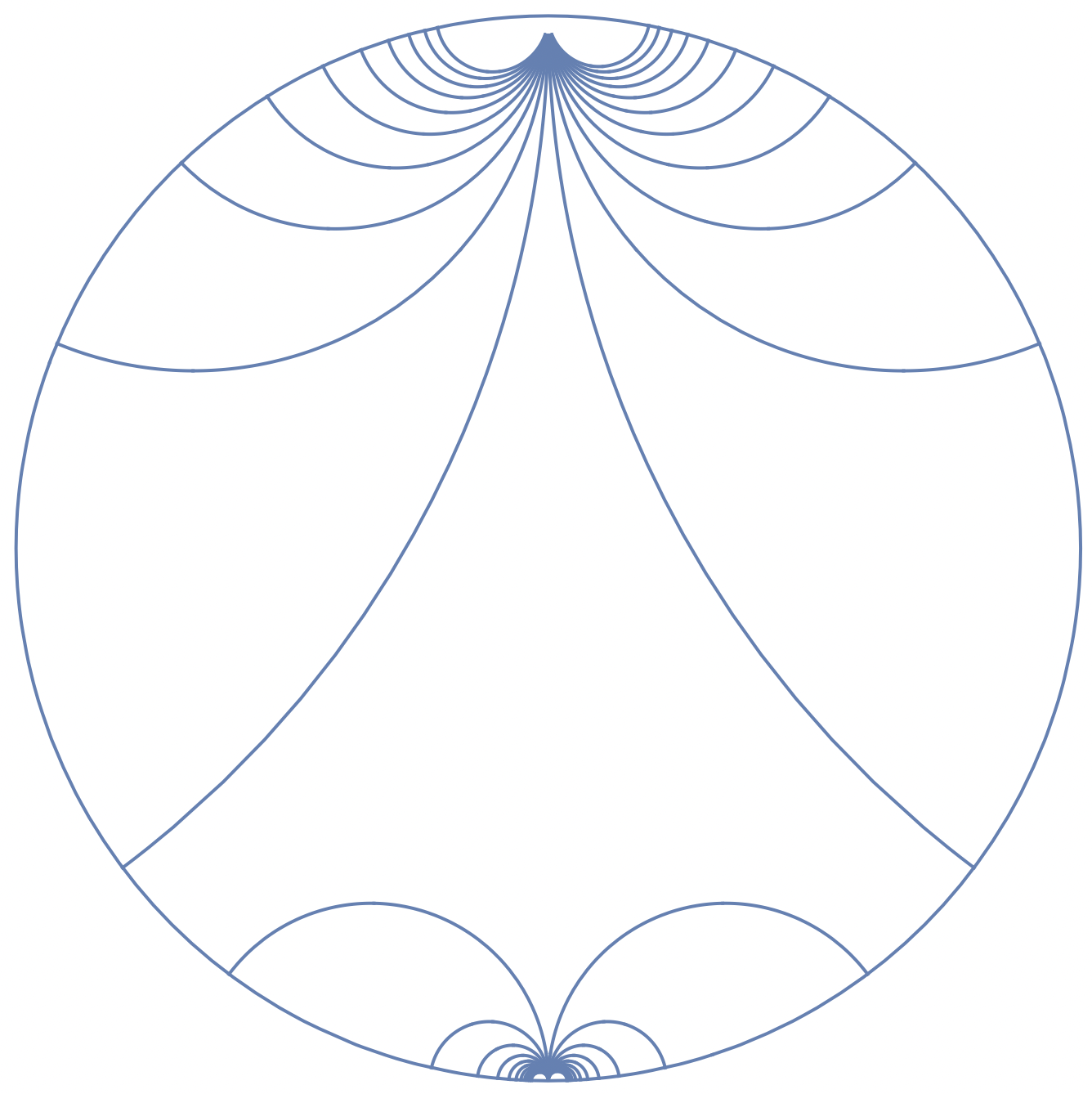
which doesn’t look anything like the original picture.

So I’m ready to give up now. What about the picture on the right? Well here I don’t even know how to begin. There is not any obvious evidence of parabolic elements, which are not only present in congruence subgroups of \(\mathrm{SL}_2(\mathbf{Z})\) but of any non-congruence subgroup as well. Perhaps there is a cusp at \(i\) with some large cusp width. There also seem to be singularities inside the disc. But that just suggests this might be a level set of a meromorphic form. But why choose a meromorphic form rather than one that is holomorphic away from the cusps? I wonder if that gives hints about the first picture; perhaps the transition from yellow to blue occurs when \(\mathrm{Im}(f)\) goes from positive to negative, and where it might be \(0\) along some geodesic arc (For example: the Fourier coefficients are rational so the form is real along the purely imaginary axis) but the form can also have imaginary part \(0\) along some non-geodesic regions and that is what one is seeing around \(-i\). That might allow one to reinterpret the graphs as something related to \(\mathrm{Im}(f)\). This suggests that the point on the left that appears to have degree four instead is related to a “local” symmetry coming from a vanishing point of the derivative of the modular function, but I’m just guessing now.

I should probably spend no more time on this, so instead I open up speculations to the comments!

Full Disclosure The picture comes with an attribution to David Lowry-Duda but I did not try to follow that lead.

Update: Perhaps it was not as obvious as intended, but the request for speculation was intended to be “how do you interpret this from the picture alone” not “send me a link” which is something which I deliberately avoided trying to do. (I will no doubt look at the way they are generated at some point in more detail.) A brief look at the LMFDB link suggests that my second explanation is pretty close, although the graph on the left is of the argument of a modular function (or rather the modular form \(\Delta\)) rather than the imaginary part. But the guess as to the explanation for the “order four” symmetry is correct, it is explained by the vanishing of \(\Delta'(\tau)\) or equivalently the vanishing of \(E_2(\tau)\) at a point on the geodesic \(1/2 + i t\). The picture on the right is still a mystery, however, and original speculations are still welcome.

Update II: So here is an new example. Like the graphs above, it plots the argument of a two modular forms on (different) finite index subgroups of \(\mathbf{SL}_2(\mathbf{Z})\). I have normalized both pictures so that the cusp width at the cusp \(i\) is the same in both cases (under the normalizations above invariant under \(\tau \rightarrow \tau + 3\); making the cusp width too small makes the behavior at \(tau = i \infty\) dominate the picture as the covolume goes up. There are dome differences with this example however:

  1. I have used (holomorphic) modular functions rather than modular forms.
  2. For these particular choices of functions, they are non-zero everywhere.
  3. I made the picture myself so it is not as pretty as the ones above.
  4. The functions I chose have the property that they are real precisely on geodesics, and thus the singularities here do form a tesselation.


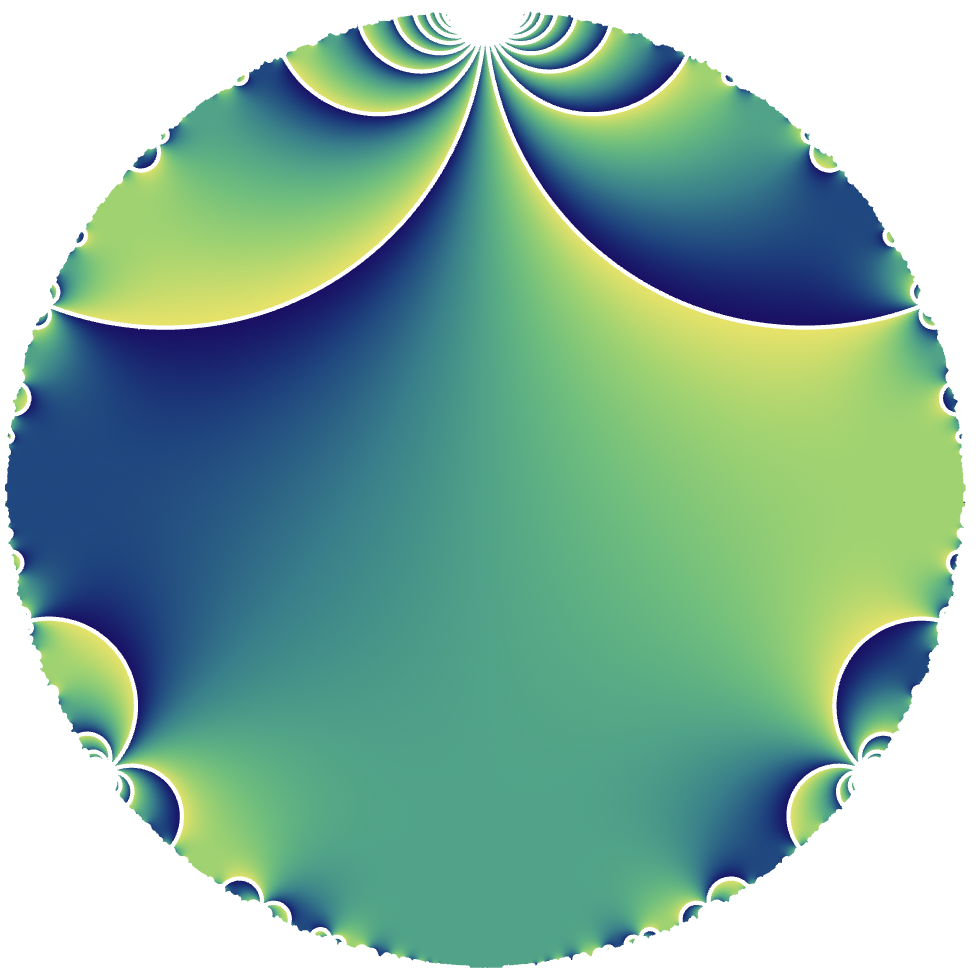
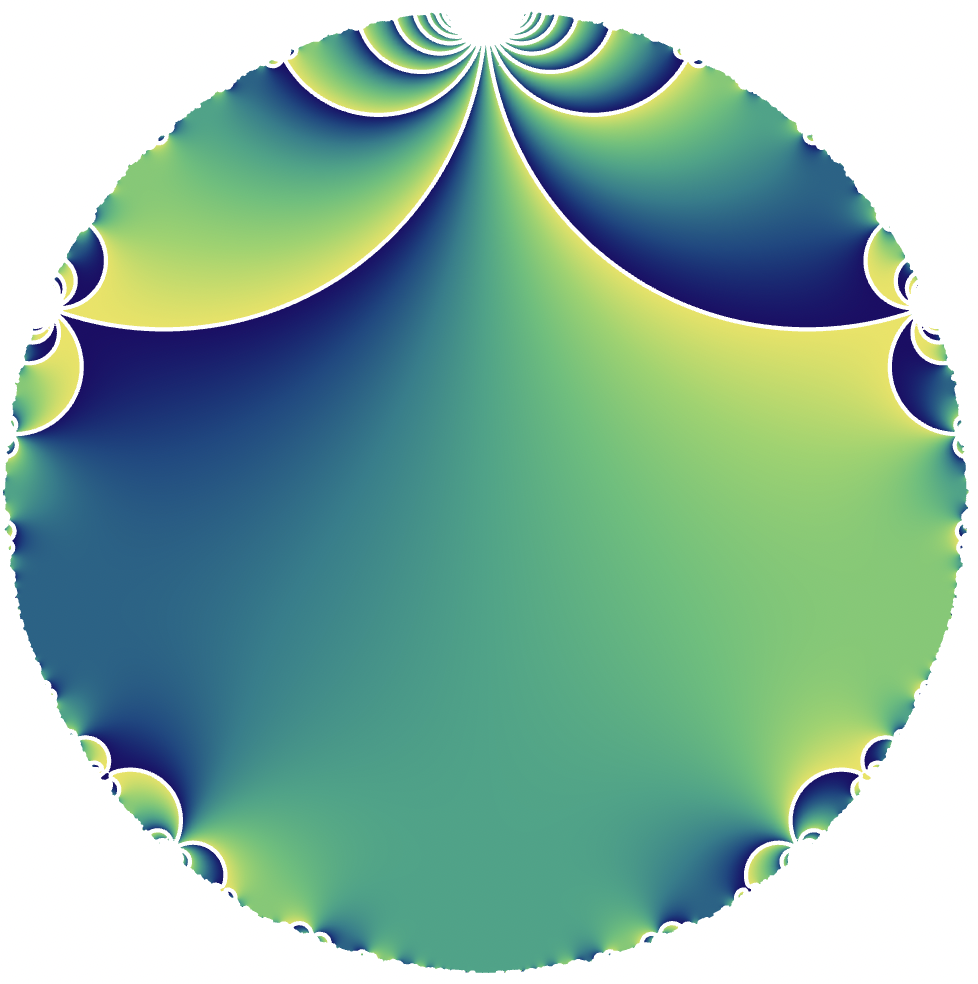
Now one of the forms is defined on a congruence subgroup and has a Fourier series in \(\mathbf{Z}[[q]]\), the other has a Fourier series in \(\mathbf{Q}[[q]]\) but not in \(\mathbf{Q} \otimes \mathbf{Z}[[q]]\) and is only defined on a non-congruence subgroup. But which is which? The pictures here are clearly much more similar than the pair of pictures above!

Posted in Mathematics | Tagged , , , , , , | 4 Comments

Boxes for Boxer update

Posted on February 28, 2023 by Persiflage

As noted in this post, exactly 42 reprints of [BCGP] were recovered in January of 2022 from boxes left out in the snow outside Eckhart Hall addressed to George Boxer. As mentioned there, the packaging (5 boxes of 8 plus a further smaller box with 2) suggested that there was a “missing box” with 8 more copies of the paper, and that one should be on the lookout at Hyde Park used book stores for the remaining copies. These reprints are after all roughly of a similar scarcity to the extant Gutenberg Bibles. Well there has been an update! My student Abhijit noted that 7 copies had been left out in the hall as an offering for graduate students (and that he had secured a copy). I initially assumed that several of my copies had escaped my hands but they all seem to be accounted for (there were 39 in my office, at least one at home, and at least one I gave to TG). So the missing box did exist after all! I still haven’t determined what happened to the box. There could have been a reprint thief who, out of guilt or madness (depending on how much of it they tried to read), was driven them to give them to the world as an attempt of repentance. Then again, the box may have ended up in someone’s hands much more unwittingly and they had only just discovered the contents. Or finally it could have been a janitor who dumped them out from a dusty closet where they had inadvertently been placed. The plot, as they say, thickens! Anonymous tips from uchicago graduate students welcome in the comments.

Posted in Rant | Tagged , , , , , | 1 Comment

What the slopes are

Posted on February 25, 2023 by Persiflage

Let \(f\) be a classical modular eigenform of weight \(k\), for example, \(f = \Delta\). The Ramanujan conjecture states that the Hecke eigenvalues \(a_p\) satisfy the bound

\(|a_p| \le 2 p^{(k-1)/2}.\)

A slightly fancier but cleaner way of saying this is as follows. Associated to \(f\) of weight \(k\), level \(N\) prime to \(p\) and finite order Nebentypus character \(\chi\) is a polynomial

\(X^2 – a_p X + p^{k-1} \chi(p).\)

(For \(\Delta\) one has \(\chi(p) = 1\) for all \(p\), but in general it can be some other root of unity.) This is the characteristic polynomial of Frobenius on the \(\ell\)-adic representation associated to \(f\) for \(\ell \ne p\), or the characteristic polynomial of crystalline Frobenius for \(\ell = p\). The Ramanujan conjecture is now that the Frobenius eigenvalues \(\alpha_p\) and \(\beta_p\) satisfy

\(|\alpha_p| = |\beta_p| = p^{(k-1)/2}.\)

This conjecture was famously proved by Deligne. Having determined the complex valuation of these eigenvalues, one might ask about their \(\ell\)-adic valuations as well. If \(\ell \ne p\), then since the polynomial above has constant term prime to \(\ell\), then \(\alpha_p\) and \(\beta_p\) are \(\ell\)-adic units. So the remaining case is \(p = \ell\).

When \(p = \ell\), the \(p\)-adic valuation of the two roots \(\alpha_p\) and \(\beta_p\) certainly satisfy \(v(\alpha_p), v(\beta_p) \ge 0\) and \(v_p(\alpha) + v_p(\beta) = k-1\). Given \(f\), we call these valuations the *slopes* of \(f\). The first observation is that the slopes depend on more than just the weight \(k\). For example, suppose that \(f\) is the weight \(2\) eigenform associated to a (modular) elliptic curve \(E\) with good reduction at \(p\), then either \(E\) has ordinary reduction, in which case the slopes are \(0\) and \(1\), or \(E\) has supersingular reduction, and the slopes are both \(1/2\).

Instead of fixing \(f\) and varying \(p\), one can fix both \(p\) and the tame level \(N\) and ask how the slopes vary as the weight changes. For example if \(N=1\) and \(p=2\), then the first interesting case is when \(k=12\) and \(f = \Delta\). In this case \(\tau(2) = 24\), and the two slopes are \(3\) and \(11-3 = 8\).

I’ve already tried to suggest by analogy to the Ramanujan conjecture why determining the p-adic valuations (the slopes) might naturally be an interesting question. But let me mention two other natural reasons. The first is that, from \(p\)-adic Hodge Theory, the crystalline eigenvalues \(\alpha_p\) and \(\beta_p\) determine the restriction of the \(p\)-adic Galois representation associated to \(f\) to the local Galois group at \(p\). The valuation of these slopes while containing less information than the eigenvalues themselves still tell you a lot about the \(p\)-adic representation, although determining exactly what is still a question of active and open interest. Secondly, as Coleman observed (following Hida in the case when one of the slopes is \(0\)), one can deform the Galois representations associated to these finite slope forms into continuous \(p\)-adic families of Galois representations associated to cuspidal eigenforms, which leads to the story of the eigencurve of Coleman-Mazur and beyond.

Gouvêa was one of the first people to undertake a numerical study of the roots.
In this paper where the slopes are, Gouvêa observed a number of interesting behavior of the slopes which were all somewhat mysterious. First, the slopes were almost all integers. This is not surprising when \(a_p(f) \in \mathbf{Z}\), but in general \(a_p(f)\) will be a random algebraic integer. The slopes also seemed to be distributed in a number of surprisings way. For example, although the slopes in weight \(k\) associated to \(f\) add up to \(k-1\), they tended to be concentrated in the intervals \([0,(k-1)/(p+1)]\) and \([p(k-1)/(p+1),k-1]\).

Kevin Buzzard went one step further and looked more closely at the slopes when \(N=1\) and \(p=2\). Ostensibly, according to Kevin, this was to test William Stein’s latest magma code for bugs! Kevin found that the slopes in this case satisfied a much more regular pattern. As mentioned above, when \(k=12\), there is a single eigenform whose smallest slope is \(3\). When \(k = 12 + 64\), there are six eigenforms whose smallest slopes are \(3, 7, 13, 15, 17, 25\), and when \(k = 12 + 2^{10}\), there are \(86\) forms whose slopes are

\(3, 7, 13, 15, 17, 25, 29, 31, 33, 37, 47, 49, 51, 57 \ldots \)

where all of these sequences are given explicitly by the \(2\)-adic valuation of \(2 ((3n)!/n!)^2\). Note that the Gouvêa-Mazur conjecture says that these sequences should have some initial segment in common, but in fact the Gouvêa-Mazur conjecture only implies that the slopes in weights \(16 + 2^6\) and \(16 + 2^{10}\) should be the same up to slope \(6\), and in practice they agree ridiculously further than this. This was all very mysterious. Kevin found a general algorithm which conjecturally computed by an inductive procedure all the slopes in all weights for a fixed tame level \(N\). (In what I always regarded as a missed opportunity, he did not call the paper “What the slopes are”).

In fact, Kevin’s conjectural answer required an assumption on \(N\) and \(p\) which for \(p>2\) was equivalent to asking that the local residual representations associated to all low-weight forms are locally reducible. For \(N=1\), the first case for which this does not happen is \(p = 59\), and this story is related to our counterexample to the original form of the Gouvêa-Mazur conjecture.

Kevin Buzzard was a speaker at the Arizona Winter School in 2001, and for his project he outlined a special case of his conjecture corresponding to overconvergent modular forms of weight \(k = 0\). Of course there are no classical modular cuspidal forms of weight \(k = 0\), but by Coleman’s theory there is a direct link between the questions about classical forms in all weights and overconvergent forms of finite slope in all weights. Kevin’s problem in its original formulation is described here.

I was a graduate student at the time, and although I wasn’t actually assigned to Kevin’s group, I did see his problem and had an idea which more or less amounted to the idea of using a slightly different explicit basis for this space than Kevin had considered and for which the \(U_2\) operator has a much nicer explicit form. In fact this basis was related to computations I had done in the summer of 93-94 and shortly afterwards during my first year at Melbourne uni, using what Matthew Emerton and I had come to definitely know as the “f” function

\(f = q \prod_{n=1} (1 + q^{n})^{24}.\)

(When It came to writing my paper with Kevin, I still felt strongly enough to insist we call it by this letter.)

Kevin and I put quite a bit of effort into proving his conjecture for more general \(k\), still with \(N=1\) and \(p=2\), but only succeeded in a few cases, including \(k = -12\), but also \(k = -84\) which was somewhat randomly chosen as a case where our approach failed but only by a little bit which could be overcome. There are a few other cases where \(X_0(p)\) has genus zero and one can do something similar, but otherwise very little progress was made on these conjectures in this situation.

There are a plethora of related conjectures which also came out (at least indirectly) from similar calculations. For example, Kevin’s algorithm certainly always produces integers, so, in light of the \(p\)-adic theory, there is the natural question of whether a crystalline representation with Hodge-Tate weights \([0,k-1]\) for \(k\) even whose residual representation is reducible always has finite slope, Then there are questions of the exact relationship between the slope and the Galois representation, and so on.

Concerning the exact slopes themselves, perhaps the biggest advance over time were refinements of Kevin’s conjecture. The Ghost Conjecture, formulated by Bergdall and Pollack, is some “master conjecture” of a combinatorial nature generalizing a number of previous conjectures concerning the slopes of classical overconvergent modular forms over the centre of weight space. (Although, perhaps amusingly, it’s not clear that these conjectures do actually imply Buzzard’s original conjecture.)

Now cut to the present day. In a recent preprint, Ruochuan Liu, Nha Xuan Truong, Liang Xiao, Bin Zhao have now proved all of these conjectures, at least up to some genericity hypotheses (excluding the case \(N=1\) and \(p=2\)!). The authors certainly employ technologies that didn’t exist 20 years ago (\(p\)-adic Langlands, for example), but that was not the only obstruction to previous progress: the paper contains a number of very original and clever ideas. Very amazingly and satisfyingly, it resolves a large number of the open problems discussed above, including Gouvêa’s conjectures about the distribution of slopes, the integrality properties of slopes for locally reducible representations, and even a version of the Gouvêa-Mazur conjecture. It is also satisfying that the arguments use \(p\)-adic local Langlands, given that some of the initial computations of slopes served at least in part as inspiration for some aspects of this program. I myself have not really worked on this circle of problems for almost 20 years but I am still very happy to see these questions answered!

Posted in Mathematics | Tagged , , , , , , , , , , , , , , | 1 Comment

Check the arXiV regularly!

Posted on February 18, 2023 by Persiflage

In a previous post, I discussed a new result of Smith which addressed the following question: given a measure \(\mu\) on \(\mathbf{R}\) supported on some finite union of intervals \(\Sigma\), under what conditions do there exist polynomials of arbitrarily large degree whose roots all lie in \(\Sigma\) whose distribution (in the limit) converge to \(\mu\)?

A natural generalization is to replace \(\Sigma\) by a subset of \(\mathbf{C}\) subject to certain natural constrains, including that \(\mu\) is invariant under complex conjugation. I decided that this had a chance of being a good thesis problem and scheduled a meeting with one of my graduate students to discuss it. Our meeting was scheduled at 11AM. Then, around 9:30AM, I read my daily arXiv summary email and noticed the preprint (https://arxiv.org/abs/2302.02872) by Orloski and Sardari solving this exact problem! There are a number of other very natural questions along these lines of course, so this was certainly excellent timing. When I chatted with Naser over email about this, he mentioned he had become interested in this problem (in part) by reading my blog post!

There is of course a general danger of giving my students problems related to my blog posts, and indeed I have refrained from posting a number of times on possible thesis problems, but in this case everything turned out quite well.

Posted in Mathematics | Tagged , , , , , | Leave a comment

Report from Australia, Part I, Coffee

Posted on February 15, 2023 by Persiflage

My travel often involves making some effort to find good local coffee. From Palo Alto to Portland, a little effort finds quality cafes with reliable espresso drinks. How does the rest of the world then stack up with Australia, the acknowledged home of coffee?

My first stop was Sydney, where my airbnb was conveniently located a stone’s throw from Skittle Lane Coffee. Many other cafes were on my list (Cabrito Coffee Traders, St Dreux Espresso Bar, and so on). What consistently stood out was not necessarily how far above in quality the coffee was from elsewhere in the world, but the sheer consistency of a cup at almost any completely random cafe in Sydney, and there are a *lot* of cafes. I mean, walking down a city street and finding three different cafes in a row was a common sight.

After a while, it began to dawn on me that I am not a coffee snob; it’s just that the rest of the world sucks when it comes to consistent espresso drinks. There are some places which can make a decent cup on occasion, but when the baristas are under pressure (especially with long lines of customers) their technique falters and they screw up the microfoam. New York City is the absolute worst in this regard — full of hipster baristas with beards to match making subpar coffee when they are rushed. So as my trip continued, I could relax and order coffee almost anywhere (country cafes, even Sydney airport). It helped that almost every single cafe had a La Marzocco coffee machine, a serious 20K piece of equipment.

All this is not to say that some coffee places were better than others. My favourite was probably Poolhouse coffee, (whose product has replaced the old coffee picture on my webpage) but this was just one great option among many.

Posted in Coffee, Travel | Tagged , , , , | Leave a comment

Potential Modularity of K3 surfaces

Posted on November 15, 2022 by Persiflage

This post is to report on results of my student Chao Gu who is graduating this (academic) year.

If \(A/F\) is an abelian surface, then one can associate to \(A\) a K3 surface \(X\) (the Kummer surface) by blowing up \(A/[-1]\) at the \(16\) singular points (corresponding to \(2\)-torsion points of \(A\). If \(F\) is a totally real field, then one knows that \(A\) is (potentially) automorphic, and it follows that \(X\) is also (potentially) automorphic, which in particular implies the Hasse-Weil conjecture for \(X\). It also proves that

\( \rho(X/F) = – \mathrm{ord}_{s=1} L(H^2(X/\overline{F},\mathbf{Q}_p(1)),s),\)

where \(H^2(X/\overline{F},\mathbf{Q}_p(1))\) is the etale cohomology group considered as a Galois representation of \(G_F\); this was conjectured by Tate in the same paper where he makes the “usual” Tate conjecture on algebraic cycles. Not all K3 surfaces arise in this way. For a start, if \(A\) has (geometric) Picard rank \(\rho(A) \ge 1\), then \(X\) has geometric Picard rank \(16 + \rho(A) \ge 17\). If the Picard rank of \(X\) is at least \(19\), then \(X\) also has to arise (at least in the category of Motives) as a Kummer surface, but more subtly this is not true in rank \(17\) and \(18\), where there are further obstructions relating to the structure of the transcendental lattice (as first observed by Morrison in this paper). What Chao does is prove the following:

Theorem: [Chao Gu] Let \(X/\mathbf{Q}\) be a K3 surface of Picard rank at least \(17\). Then \(X\) is potentially automorphic, and the Hasse-Weil conjecture holds for \(X\).

In the most interesting case of rank \(17\), the approach is to lift the compatible family of \(5\)-dimensional orthogonal representations associated to the transcendental lattice to a compatible family of \(4\)-dimensional symplectic representations which one hopes to prove is potentially automorphic. Finding (motivic) lifts of K3 surfaces is a well-studied problem, and a nice analysis of what happens arithmetically can be found in Patrikis’ thesis. From the Kuga-Satake construction, one can certainly reduce to considering certain abelian varieties. The question is then narrowing down the precise endomorphism structures of these varieties as well as their fields of definition. It turns out that for the problem of interest, there are more or less three types of abelian varieties one might want to consider beyond abelian surfaces over a totally real field \(F\):

  1. Abelian varieties \(A/F\) of dimension \(2d\), where \(A\) admits endomorphisms by an order in the ring of integers of a totally real field \(E\) of degree \([E:\mathbf{Q}] = d\).
  2. Abelian surfaces \(A/H\) over some Galois extension \(H/F\) where the conjugate of \(A\) by \(\mathrm{Gal}(H/F)\) are all isogenous over \(H\).
  3. Abelian \(4\)-folds \(A/F\) with endomorphisms by an order in a quaternion algebra \(D/\mathbf{Q}\).

More generally, one needs to consider the “cross-product” where several (or all) of these phenomena may occur at once. For those more familiar with the story of two-dimensional Galois representations over \(\mathbf{Q}\), these three extensions correspond to replacing elliptic curves over \(\mathbf{Q}\) by abelian varieties of \(\mathrm{GL}_2\)-type, to \(\mathbf{Q}\)-curves, and to fake elliptic curves respectively. It turns out that the last case doesn’t happen over totally real fields but the analog for abelian surfaces does, requiring certain conjectures to be modified.

The optimal generalization of Boxer-Calegari-Gee-Pilloni to this setting would be to prove that all of these varieties are potentially modular. However, it turns out that there is an obstruction to proving this: namely, is not always possible to prove that these varieties have enough ordinary primes (one needs something slightly stronger, namely ordinary primes whose unit eigenvalues are distinct modulo \(p\)). This puts some restrictions on what can be proved unconditionally, but everything works as long as there are enough ordinary primes. Chao’s proof requires a number of modifications from [BCGP], in particular to the Moret-Bailly part of the argument. In our original paper, we exploited the fact that we were working only with abelian surfaces which allowed us to use some tricks to simplify this step. In particular, the problem of finding an appropriate point on
the desired moduli space over \(\mathbf{Q}_p\) was made much simpler by virtue of the fact that the original abelian surface produced such a point. In Chao’s generalization, however,
this trick doesn’t work, and one must use more subtle arguments using Serre–Tate theory. Fortunately, enough tricks are available concerning ordinary primes to settle the general case of K3 surfaces of (geometric) Picard rank at least \(17\) when they are defined over \(\mathbf{Q}\). But note there do exist many such K3 surfaces (not related to abelian surfaces) over \(\mathbf{Q}\) that one can write down explicitly; see the examples due to Nori discussed in Section 9.4.

Note that this result is new even for Picard rank \(18\). For Picard rank \(19\) and \(20\), the (potential) modularity of any \(X/F\) for a totally real field \(F\) reduces to the corresponding problem for elliptic curves. The case of Picard rank \(16\) appears as hopeless as the case of generic genus three curves.

Posted in Mathematics, Work of my students | Tagged , , , , , , , , | 2 Comments

Peak Hyde Park

Posted on November 12, 2022 by Persiflage

Me dressed as a crocodile chasing the Groke while being chased by Drinfeld down Harper Ave on Halloween (all in front of a 16 foot inflatable pumpkin). Sadly, Drinfeld was not dressed as a Shtuka.

The Groke

Posted in Travel | Tagged , , , , | Leave a comment

The future is now; recap from Cetraro

Posted on July 31, 2022 by Persiflage

I’ve just returned from the second Journal of Number Theory biennial conference in Italy. It’s always nice to get a chance to see slices of number theory one wouldn’t otherwise see at the conferences I usually go to (although this was the first conference of any kind I attended in person since 2019). Here is a brief and incomplete recap.

  • There were more talks that mentioned the Manin-Mumford conjecture and its various generalizations (particularly to uniform bounds in families) than I have ever previously attended in my life. There were probably equally many talks which mentioned Ax-Schanuel as well. It was nice to see these subjects and I learnt quite a lot from these talks.

  • In the talk I linked to in the last post, I claimed that the modularity of elliptic curves over the Gaussian integers is “within our grasp”; well, the future is now! James Newton talked about his work in progress with Ana Caraiani where they prove modularity of all curves over imaginary quadratic fields \(F\) such that \(\# X_0(15)(F) < \infty\), which includes \(\mathbf{Q}(\sqrt{-1})\). One of the key tools in their proof is a suitable local-global compatibility statement for Galois representations coming from torsion classes in the crystalline setting where one is not in the Fontaine-Laffaille range (because of ramification in the base, for example). This was a situation where I had even been hesitant to make a precise conjecture. The problem is that the natural conjecture one might want to make is that the map of Hecke algebras factors locally through the Kisin deformation rings. But the construction of Kisin deformation rings as closures which are flat over \(W(k)\) by default might make one worried whether it is the correct integral object for torsion representations. But Caraiani and Newton show that such concerns are unfounded, and the \(W(k)\)-flat deformation rings are indeed the correct objects. One key point of their argument is showing that the (possibly torsion) representations \(\rho \oplus \rho^{\vee}\) (for suitable twists of \(\rho\) occur inside the cohomology of the Shimura variety in such a way where (using some notion of ordinary for a parabolic other than the Borel) the local representations in characteristic zero are reducible and realize the required crystalline lifts of each factor. One remaining annoyance is that one would like to find points over twists \(X(\overline{\rho}_E,\wedge)\) of the Klein quartic \(X(7)\) over \(F\) corresponding to \(E[7]\) which lie on solvable CM fields (in order to do a switch at the prime \(7\). You could (for example) start with the point \(E\) and the \(15\)-isogenous curve \(E’\) and connect them via a line. This line will go through two further points defined over a quadratic extension \(H/F\), but there is no reason to suppose a quadratic extension of an imaginary quadratic field will be CM. I had some idea related to a half-forgotten fact I learnt from John Cremona walking in the woods near Oberwolfach, but upon further consideration this half-forgotten fact was sufficiently ephemeral that it could not be reconstructed and didn’t appear to correspond to any actual facts. I did learn from Tom Fisher the nice fact that the four curves \(3\)-isogenous to \(E\) are collinear on the curve \(X(\overline{\rho}_E),3 \wedge)\) corresponding to the same mod-\(7\) representation with the other choice of symplectic form (that is, \(\wedge\) scaled by a quadratic non-residue).

  • This was my first chance seeing a talk on the work of Loeffler-Zerbes on BSD for abelian surfaces. The most difficult condition to verify in their theorem is that a certain (characteristic zero) deformation problem is unobstructed. It seems very plausible to me that one could numerically verify some interesting examples and get truly unconditional results on BSD for some autochthonous abelian surfaces, or at least autochthonous elliptic curves over imaginary quadratic fields. The idea is that to prove a certain ordinary (of some flavour) deformation problem is unobstructed it suffices to prove that it is unobstructed modulo \(p\), which reduces to a computation with ray class groups in the splitting field of \(\overline{\rho}: G_{\mathbf{Q}} \rightarrow \mathrm{GSp}_4(\mathbf{F}_p)\). This seems within the realm of practicality. Moreover, once one verifies the condition for \(A\), one immediately deduces it for all the twists of \(A\) as well. It is important here to take \(p\) small, that is at most \(3\). Certainly if the mod-\(3\) image is surjective the extension will be too large, but the case of a representation induced from an imaginary quadratic field seems completely manageable. The other possibility is to work with \(p=2\). Here I think one should work with \(H^1(\mathbf{Q},\mathrm{ad}_0(\overline{\rho}))\) where \(\mathrm{ad}_0\) is the quotient of the \(11\)-dimensional adjoint representation by the diagonal (so slightly different from trace zero matrices). Here I’m imagining starting with a modular abelian surface which has good ordinary at \(2\) and whose mod-\(2\) image is \(S_5\). It might also be convenient if the local factor at \(2\) is congruent to \((1+T+T^2)T^2 \bmod 2\) so that the local deformation problem has good integral properties. Anyone interested in computing such an example?

  • During the conference the second “David Goss Prize” was awarded. This prize is for work done in the past two years in number theory by someone at most 35(!) and also by someone who has not (yet!) won any other major prizes. (I joked that it might be nice to have a prize for people 50 or older who have not won any prizes but there is something nice about no longer being eligible for any prize except those one has no hope of winning.) This year’s winners were Ziyang Gao and Vesselin Dimitrov. The laudatio is here and a live action photo is here:

    Goss Prize

    Congratulations to both!

    Talking of prizes, I can’t quite work out whether there are far more prizes than there used to be, or whether I was simply oblivious about them when I was younger.

  • Sad to say that the coffee I had in Italy was basically not that good. I’m prepared to make the seemingly heretical claim that nowadays it’s much easier to get excellent coffee in London. (Obviously it’s much easier to get excellent coffee in Melbourne.) The Pizza is still great though, and Mercato Centrale Roma ranks as the best food I have ever eaten in a train station.

  • I dropped my iPhone one too many times and ended up with a broken phone with three blindingly white strips running down the right hand side of the screen. At first it did not respond to any touch at all, but after a few hours it started responding to touches on roughly the left 2/3 of the screen. There were just enough applications which were compatible with rotating the screen (so the relevant buttons came within reach) that it was barely usable for the remainder of the trip. (Other peculiarities: it gobbled battery power at an immense speed to the extend that it would last only an hour or two unused without being charged.) It did mean I started using Siri for the first time, although Siri was unsurprisingly useless for doing things I actually wanted (like “pressing” buttons on the screen that I couldn’t touch myself). The phone was also in the habit of randomly acting as if it was being pressed all on its own. The worst example of this was when trying to check into my flight on the way home. As my flight was delayed (well in advance) by several hours, the app was pushing for users to change to a different flight. To my horror, the app randomly started acting as if buttons were being pressed and changed my direct flight to Chicago (upgraded to business class) leaving in the early afternoon to an economy ticket leaving at 8:00AM in the morning and going through Dallas. When I called American they (at first) said that I couldn’t change it back because the original flight was now sold out, but some further negotiation finally got me back on my original flight. So I got to have one pleasant evening in Rome dining on the Piazza Navona after an obligatory trip to the local toy store.
Posted in Mathematics, Travel | Tagged , , , , , , , , , , , , , , , | 5 Comments

30 years of modularity: number theory since the proof of Fermat

Posted on July 8, 2022 by Persiflage

It’s probably fair to say that the target audience for this blog is close to orthogonal to the target audience for my talk, but just in case anyone wants to watch it in HD (and with the audio synced to the video) on I have uploaded it to youtube here:

Posted in Mathematics | Tagged , , , , , , , , , , , , , , , , , , , , , , , , | 13 Comments

Locally induced representations

Posted on June 16, 2022 by Persiflage

Today is a post about work of my student Chengyang Bao.

Recall that Lehmer’s conjecture asks whether \(\tau(p) \ne 0\) for all primes \(p\), where

\(\Delta = q \prod_{n=1}^{\infty} (1 – q^n)^{24} = \sum \tau(n) q^n\)

is Ramanujan’s modular form. You might recall that Naser Talebizadeh Sardari and I studied a “vertical” version of Lehmer’s conjecture where instead of fixing a modular form, we fixed a prime \(p\) and a tame level \(N\) and showed that there were only finitely many normalized eigenforms \(f\) of level \(N\) and even weight \(k\) with \(a_p(f) = 0\) which were not CM. We exploited the fact that such forms give rise to Galois representations

\(\rho: G_{\mathbf{Q}} \rightarrow \mathrm{GL}_2(\overline{\mathbf{Q}}_p)\)

which are crystalline at \(p\) but also locally induced at \(p\) from the unique unramified quadratic extension \(K/\mathbf{Q}_p\). As explained in this post, it’s hard to see this method being able to say much more to this (for example, to say anything about Lehmer’s actual conjecture), since there do actually exist non-CM forms with \(a_p(f) = 0\).

In practice, we don’t even know in level \(N=1\) whether there exist infinitely many normalized eigenforms \(f\) with \(a_p(f) \equiv 0 \bmod p\). As mentioned in this post, one source of such representations comes from modular forms with exceptional image. For example, if \(f = \Delta E_4\) is the normalized eigenform of weight \(16\), then as first observed by Serre and Swinnerton-Dyer, the mod-\(59\) representation

\(\overline{\rho}_{f}: G_{\mathbf{Q}} \rightarrow \mathrm{GL}_2(\overline{\mathbf{F}}_p)\)

has projective image \(S_4\) coming from the splitting field of \(x^4 – x^3 – 7 x^2 + 11 x + 3\). But the local residual representation in this case is induced, which implies that \(a_{59} \equiv 0 \bmod 59\). As explained in that post, standard conjectures about primes predict that there should be infinitely many \(S_4\)-representations unramified outside a single prime \(p\) giving rise to modular Galois representations which will then come from level one modular forms \(f\) with \(a_p(f) \equiv 0 \bmod p\).

Chengyang’s work concerns examples precisely of this sort. From my work with Naser, we can deduce that there are at most finitely many \(f\) of level one with \(a_{59}(f) = 0\). Chengyang proves that there are no such forms. More precisely:

Theorem [Bao] Suppose that \(f\) is a modular form of level one, and suppose that \(a_p(f) = 0\). Then all of the residual mod-\(p\) representations \(\overline{\rho}\) associated to \(f\) have big image, that is, image containing \(\mathrm{SL}_2(\mathbf{F}_p)\).

In other words, none of the (presumably many) infinite examples of \(S_4\) representations giving rise to \(f\) of level one with \(a_p(f) \equiv 0 \bmod p\) can ever give an \(f\) with \(a_p(f) = 0\).

Chengyang also proves some further results about the deformations of representations with exceptional image. For example, for the mod-\(59\) representation above, the only deformations to characteristic zero unramified outside \(p=59\) which are locally induced are the representations which up to twist are the ones which up to twist coincide with the unique lift with finite image and order prime to \(p=59\).

In contrast, one might ask what happens for \(p=79\), the next case where there exists a form \(f\) of level one with \(a_p(f) \equiv 0 \bmod p\). I suspect that in this case a (possibly quite complicated computation) should show that there should be at most one form with \(a_p(f) = 0\), but that it might be quite difficult to prove using \(p\)-adic methods that there are no such forms. The problem will be that there will exist a deformation which will have infinite image and be locally induced, but now it will have generalized Hodge–Tate weights \([0,\kappa]\) for some \(p\)-adic number \(\kappa\) for which it will be very hard to show is not an integer. This is analogous to the family of Eisenstein series of level one with \(p = 37\). One knows that the \(p\)-adic zeta function will have a unique zero, but it is very hard to probe the arithmetic nature of that zero and to rule out it occurring at some arithmetic weight. To put this slightly differently, is there an integer \(k \ge 1\) such that

\(\zeta_{37}(-31 + 36 k) = 0?\)

Presumably not, but this seems extremely difficult; the difficulty of course is that there will be a solution with \(k \in \mathbf{Z}_{37}\).

Posted in Mathematics, Students, Work of my students | Tagged , , , | 1 Comment